sankalpmittal
- 785
- 27
Homework Statement
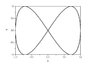
The two linear simple harmonic motions of equal amplitudes , and angular frequencies ω and 2ω are imposed on a particle along the axes of X and Y respectively. If the initial phase difference between them is π/2 , then find the resultant path followed by the particle.
Homework Equations
http://en.wikipedia.org/wiki/Simple_harmonic_motion
The Attempt at a Solution
I tried solving question using x= a sinωt
And other is y=a sin(2ωt + π/2)
Solving them , I get the wrong answer in terms of x and y...
Please help !
Thanks in advance...