R A V E N
- 63
- 0
I have one confusing issue to resolve:
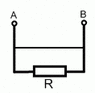
What is the resistance between points A and B in simple system illustrated in attachment?Wouldn`t be logical to assume that it is 0,as current strives to flow through path with lowest possible resistance,if I understood it correctly?
Yes,I know that real transmission lines have some resistance,but in network anaylsis their resistance is considered to be equal to zero.
What is the resistance between points A and B in simple system illustrated in attachment?Wouldn`t be logical to assume that it is 0,as current strives to flow through path with lowest possible resistance,if I understood it correctly?
Yes,I know that real transmission lines have some resistance,but in network anaylsis their resistance is considered to be equal to zero.
Attachments
Last edited: