jonjacson
- 450
- 38
Homework Statement
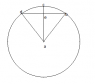
I don't know the radius of the circumference. I could only measure the arc lenght, and the height. I know the guidelines say we should not post images, but this is a geometric problem and I think it is something logic to show it with a picture.
So the variables are the distances Radius R of the circumference, distance ce also called sagitta, and arc length of the circumference from point d to point b.
I know the arc length from d to b and the distance ce, and I want to calculate the radius R of the circumference.
Homework Equations
Basic trigonometric functions:
Arc= Radius * Angle
Cos \alpha = adjacent side/ hypotenuse
The Attempt at a Solution
Well, I get an equation, but I don't know to solve it. I hope you can check if my calculations are right and then if there is any method to get the answer R.
Distance ca= Radius R
Distance ce= It is known, it is the sagitta.
Distance ea= R - ce
And now looking at the triangle aeb, I want to calculate the angle between ea and ba sides.
Simply using cosine function:
cos \alpha = (R - ce)/ba = (R - ce)/R
So the angle \alpha = ArcCos ( (R - ce)/R)
Now I will use the equation Arc= Radius * Angle, in this case:
Arc= from point d to point b
Angle= angle between sides da and ba, which is equal to two times the angle \alpha we have just calculated.
So we have:
Arc= Radius * 2*ArcCos((R-ce)/R)
And the problem is that I have R inside the argument of the trigonometric function, and at the same time it is multipliying the trigonometric function, so I cannot get an equation of R as function of ce and the Arc, I don't know how to proceed.
I tried to solve it with Mathematica but I got an error, even if I used a numerical solver. At this point I don't know how to solve R.
Thanks to everybody!