Rain and man problem. (relative motion)

AI Thread Summary
The problem involves calculating the velocity of rain with respect to a man moving at 6 km/h due east, while the rain falls vertically at 4 km/h relative to the man. By applying Pythagorean theorem, the actual velocity of rain can be determined as it forms a right triangle with the man's velocity. The velocity of rain relative to the man is perpendicular to the ground, allowing for straightforward calculations. This approach emphasizes the importance of relative motion in understanding the dynamics of the situation. The final calculation yields the actual velocity of the rain.
Aakaersh
Messages
1
Reaction score
0
Please help me with the following problem...

rain.jpg
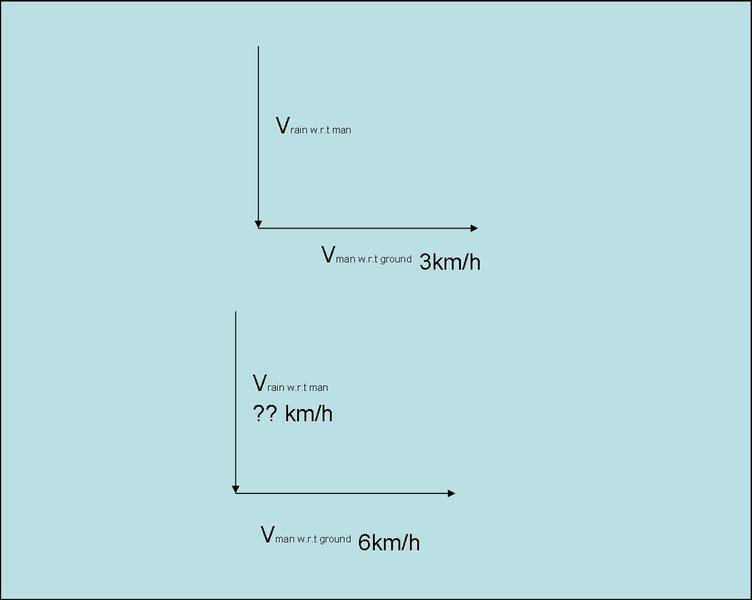velocity of man wrt to ground is 3km/h due east. velocity of rain with respect to man is 4km/h and falls vertically downwards. If the man moves at 6km/hr then the velocity of rain wrt to man is?
 
Physics news on Phys.org
By using Pythagoras, you can find the actual velocity of rain. And then use it in the next case. Here, as V of rain wrt man is perpendicular to ground, you can constuct a triangle to find actual velocity of rain.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Is this a reference frame problem ?
Replies
5
Views
1K
Relative Velocity (Man walking in rain question)
Replies
4
Views
7K
Optimizing Velocity on Incline for Vertical Rain Perception
Replies
5
Views
2K
Find the velocity of the rain drops with respect to the man?
Replies
4
Views
2K
Classic rain falling on a car's window problem doubt
Replies
2
Views
4K
Does a man jumping off a rolling cylinder affect its velocity?
Replies
5
Views
1K
Needs clarity on this displacement vector diagram
Replies
3
Views
953
Uniform Motion in 2D - A man chasing a bus
Replies
20
Views
1K
What Is the Speed of the Man Relative to the Ground?
Replies
11
Views
2K
Finding the Speed of Rain in Relative Motion
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top