maryhem
- 1
- 0
Challenging Ramp and Pulley Problem
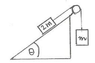
Two blocks of masses 2m and m are connected by a weightless string over a frictionless, massless pulley, as shown in the figure. The coefficient of kinetic friction between the block and the incline is \mu. The system is in a uniform gravitational field directed downward of strength g. Find the incline angle \theta such that the blocks move at a constant speed. Distinguish between the cases of upward and downward motion. Rationalize your solutions using a simple physical picture.
\mathbf{F} = m\mathbf{a}
So we start by looking at the forces acting on each block. In this case, we will be looking at downward motion. For the 2m mass:
2mg\sin\theta - \mu mg\cos\theta - T = 0
And for the second block:
T - mg = 0 \implies T = mg
Using the second equation and plugging into the first equation, we find:
2\sin\theta - 2\mu\cos\theta = 1
I can't figure out how to solve for \theta. Wolfram's answer is pretty ugly.
Homework Statement
Two blocks of masses 2m and m are connected by a weightless string over a frictionless, massless pulley, as shown in the figure. The coefficient of kinetic friction between the block and the incline is \mu. The system is in a uniform gravitational field directed downward of strength g. Find the incline angle \theta such that the blocks move at a constant speed. Distinguish between the cases of upward and downward motion. Rationalize your solutions using a simple physical picture.
Homework Equations
\mathbf{F} = m\mathbf{a}
The Attempt at a Solution
So we start by looking at the forces acting on each block. In this case, we will be looking at downward motion. For the 2m mass:
2mg\sin\theta - \mu mg\cos\theta - T = 0
And for the second block:
T - mg = 0 \implies T = mg
Using the second equation and plugging into the first equation, we find:
2\sin\theta - 2\mu\cos\theta = 1
I can't figure out how to solve for \theta. Wolfram's answer is pretty ugly.
Attachments
Last edited: