Paul P
- 2
- 0
hi,
i have some question and i hope someone know answers:
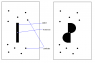
Lets have closed two dimensional space with some particles, which have random position and random velocities. In the center of space is object, which has central fixed axis. This object has no velocity and no angular velocity. (see left side of attached image) That is starting state of system. After some time T, during which particles and object flexible bounces and central object make only rotational movement, system ends in some state.
my question is 1.) When time T is long enough, what is angular displacement of central object during time T ?
// i think close to zero ?
Lets change situation little bit. Take away central object and replace with another shaped object - see right side of attached image.
question is same 2.) When time T is long enough, what is angular displacement of shaped central object during time T ?
// i think, that shaped object will prefer rotate counterclockwise ... or not ?
thanks for answers
i have some question and i hope someone know answers:
Lets have closed two dimensional space with some particles, which have random position and random velocities. In the center of space is object, which has central fixed axis. This object has no velocity and no angular velocity. (see left side of attached image) That is starting state of system. After some time T, during which particles and object flexible bounces and central object make only rotational movement, system ends in some state.
my question is 1.) When time T is long enough, what is angular displacement of central object during time T ?
// i think close to zero ?
Lets change situation little bit. Take away central object and replace with another shaped object - see right side of attached image.
question is same 2.) When time T is long enough, what is angular displacement of shaped central object during time T ?
// i think, that shaped object will prefer rotate counterclockwise ... or not ?
thanks for answers