wmac
- 19
- 0
Hello,
I am trying to find a clean solution for this (i.e. straightforward and academically acceptable). I appreciate if someone can help me.
1- I need to select between selections 1 to n (in my case 1-8 ). However each preceding item should have higher probability than the next one. For example, first item should have higher probability than the 2nd and the 2nd should have higher than the 3rd one etc.
I also need a parameter which enables me to adjust the probability of the first item. (i.e. the slope of the curve and therefore the distribution of probability)
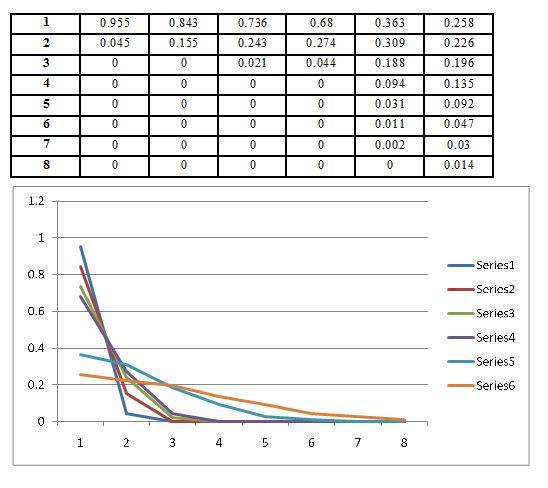
What distribution with what parameters I should use.
2- Currently I use a normal distribution with mean value of 1 and different sigmas. When generating random numbers (float) I ignore numbers lower than 1 and then round up numbers higher than that to my discrete choices (i.e. 1-8 ).
Describing this in an academic paper is unacceptable I guess. So I am looking for a proper clean method (ideally a specific distribution with a few parameters).
Thanks in advance.
I am trying to find a clean solution for this (i.e. straightforward and academically acceptable). I appreciate if someone can help me.
1- I need to select between selections 1 to n (in my case 1-8 ). However each preceding item should have higher probability than the next one. For example, first item should have higher probability than the 2nd and the 2nd should have higher than the 3rd one etc.
I also need a parameter which enables me to adjust the probability of the first item. (i.e. the slope of the curve and therefore the distribution of probability)
What distribution with what parameters I should use.
2- Currently I use a normal distribution with mean value of 1 and different sigmas. When generating random numbers (float) I ignore numbers lower than 1 and then round up numbers higher than that to my discrete choices (i.e. 1-8 ).
Describing this in an academic paper is unacceptable I guess. So I am looking for a proper clean method (ideally a specific distribution with a few parameters).
Thanks in advance.