jankod
- 2
- 0
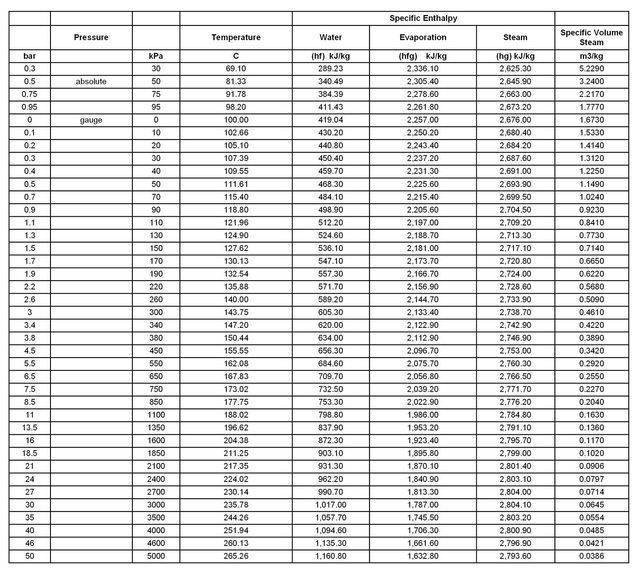
Looking at the steam table below, if I understand things correctly, it will take 419kJ to bring a kg of water to the boil at 100°C and a further 2257kJ to turn all of that boiling water into steam.
I assume that would have to be in an open boiler, as the pressure inside of a closed vessel would increase, in turn increasing the boiling point of the water.
But in the simple case of an open boiler, does the rate of steam generation (as in kg/s or m3/s) remain constant during the time it takes to boil away that water?
From the table, I would deduce that 210kJ would bring 0.5kg of water to the boil and a further 1128kJ would evaporate all of it, but does that mean 1128kJ would evaporate half of 1kg of boiling water?
I assume that would have to be in an open boiler, as the pressure inside of a closed vessel would increase, in turn increasing the boiling point of the water.
But in the simple case of an open boiler, does the rate of steam generation (as in kg/s or m3/s) remain constant during the time it takes to boil away that water?
From the table, I would deduce that 210kJ would bring 0.5kg of water to the boil and a further 1128kJ would evaporate all of it, but does that mean 1128kJ would evaporate half of 1kg of boiling water?
Last edited: