Ratio of the length of resistive wires in a square

[Krushnaraj Pandya]

Homework Statement

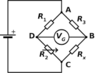
In a given square ABCD each side is of 1 m and resistance of wire is 1 ohm/m. A resistance of 1 m is connected from A to E (which lies on side CD). A constant potential difference is applied across A and C, if potentials of B and E are same then find CE/ED.

Homework Equations

V=IR, kirchhoffs laws

The Attempt at a Solution

The complete solution is given as a solved example in my book, as per the attached picture. They've treated it as a balanced wheatstone bridge even though the bridge is ADC (which is just a parallel connection with ABC and AEC) instead of across BE like required in a wheatstone bridge- can someone explain this discrepancy? Pardon the image quality, I only have a webcam. The takeaway from the figure is that they wrote R(AE)/R(AB) = R(CE)/R(CB) and I don't understand how.

 

[BvU]

even though the bridge is ADC (which is just a parallel connection with ABC and AEC) instead of across BE like required in a wheatstone bridge

No. B and E are the 'side points', A and C are the 'top and bottom'

 

[Krushnaraj Pandya]

No. B and E are the 'side points', A and C are the 'top and bottom'

The bridge should be across the side points- And its not across B and E.

 

[haruspex]

View attachment 234295 The bridge should be across the side points- And its not across B and E.

You are told the potentials are the same at B and E. So add the bridge BE and you have a balanced Wheatstone bridge.

 

[Krushnaraj Pandya]

You are told the potentials are the same at B and E. So add the bridge BE and you have a balanced Wheatstone bridge.

Ohh! Right!, I understand, thank you very much