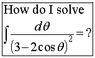- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Integrating Rational Functions: How to Solve Challenging Integrals?
In summary, the conversation involves two individuals discussing the solution to a difficult integral. After various attempts and suggestions, one of them finally finds the correct solution using the Heaviside Method and a substitution. They also discuss the use of partial fractions and its limitations. Eventually, they reach a conclusion that only rational functions can be solved using partial fractions.
Physics news on Phys.org
- #2
- 13,350
- 3,128
I've struggled with it and i couldn't come up with an answer.All i can tell u is that it cannot be factorized (decomposed in simple fractions) because it's not rational.The square in the denominator is the most annoying... 
Daniel.
Daniel.
- #3
bomba923
- 763
- 0
Wait..sorry neverm0nd----i found a solution!
Just use the Heaviside Method and make A, B, C--
substitute x= cos (theta)
and that dx= -sin (theta)
and then divide by the -sin (theta) as -(1-x^2)
-----------------------------
put A/((3-2x)^2)+B/((1+x)^(1/2))+C/((1-x)^(1/2),
then solve using heaviside
Just use the Heaviside Method and make A, B, C--
substitute x= cos (theta)
and that dx= -sin (theta)
and then divide by the -sin (theta) as -(1-x^2)
-----------------------------
put A/((3-2x)^2)+B/((1+x)^(1/2))+C/((1-x)^(1/2),
then solve using heaviside
Last edited:
- #4
- 13,350
- 3,128
I told u it doesn't work...
[tex] \int \frac{d\theta}{(3-2\cos\theta)^{2}} [/tex]
,via the substitution
[tex] \cos\theta\rightarrow x [/tex]
becomes
[tex] -\int \frac{dx}{\sqrt{1-x^{2}}(3-2x)^{2}} [/tex]
which is very irrational.
So your
[tex] \frac{A}{(3-2x)^{2}}+\frac{B}{\sqrt{1-x}}+\frac{C}{\sqrt{1+x}} [/tex]
doesn't lead anywhere.
Daniel.
[tex] \int \frac{d\theta}{(3-2\cos\theta)^{2}} [/tex]
,via the substitution
[tex] \cos\theta\rightarrow x [/tex]
becomes
[tex] -\int \frac{dx}{\sqrt{1-x^{2}}(3-2x)^{2}} [/tex]
which is very irrational.
So your
[tex] \frac{A}{(3-2x)^{2}}+\frac{B}{\sqrt{1-x}}+\frac{C}{\sqrt{1+x}} [/tex]
doesn't lead anywhere.
Daniel.
- #5
Inquisitive_Mind
- 11
- 0
Use t method? (i.e. set t=tan(x/2), such that cos(x)=(1-t^2)/(1+t^2))
- #6
marlon
- 3,792
- 11
Inquisitive_Mind said:Use t method? (i.e. set t=tan(x/2), such that cos(x)=(1-t^2)/(1+t^2))
This is the right way. I got to a solution like this. Besides the new differential shall be 2dt/(1+t²). Then you can manipulate this integral so that you will get two integrals. One of them is elementary (arcustangens)and the other one can be soved with partial integration...
Just try it...
remember with manipulation i mean something like this [tex]\frac {1+t^2}{(1+5t^2)^2} = \frac{1+ 5t^2}{(1+5t^2)^2} + \frac{-4t^2}{(1+5t^2)^2}[/tex]
marlon
- #7
marlon
- 3,792
- 11
dextercioby said:I told u it doesn't work...
[tex] \int \frac{d\theta}{(3-2\cos\theta)^{2}} [/tex]
,via the substitution
[tex] \cos\theta\rightarrow x [/tex]
becomes
[tex] -\int \frac{dx}{\sqrt{1-x^{2}}(3-2x)^{2}} [/tex]
which is very irrational.
So your
[tex] \frac{A}{(3-2x)^{2}}+\frac{B}{\sqrt{1-x}}+\frac{C}{\sqrt{1+x}} [/tex]
doesn't lead anywhere.
Daniel.
And besides this decomposition is even wrong. You did not apply the rules correctly...But drop it because it is useless here and certainly with the sqrt you CANNOT do this !
marlon
- #8
- 13,350
- 3,128
I knew the decomposition was wrong,i told him that substitution would lead nowhere.
Anyways,my result is
[tex] \int \frac{d\theta}{(3-2\cos\theta)^{2}}=\frac{4}{5}\frac{\tan\frac{\theta}{2}}{1+5\tan^{2}\frac{\theta}{2}}+\frac{6\sqrt{5}}{25}\arctan(\sqrt{5}\tan\frac{\theta}{2})+C [/tex]
Daniel.
Anyways,my result is
[tex] \int \frac{d\theta}{(3-2\cos\theta)^{2}}=\frac{4}{5}\frac{\tan\frac{\theta}{2}}{1+5\tan^{2}\frac{\theta}{2}}+\frac{6\sqrt{5}}{25}\arctan(\sqrt{5}\tan\frac{\theta}{2})+C [/tex]
Daniel.
- #9
marlon
- 3,792
- 11
dextercioby said:I knew the decomposition was wrong,i told him that substitution would lead nowhere.
Anyways,my result is
[tex] \int \frac{d\theta}{(3-2\cos\theta)^{2}}=\frac{4}{5}\frac{\tan\frac{\theta}{2}}{1+5\tan^{2}\frac{\theta}{2}}+\frac{6\sqrt{5}}{25}\arctan(\sqrt{5}\tan\frac{\theta}{2})+C [/tex]
Daniel.
You see, my trick worked...
marlon
- #10
bomba923
- 763
- 0
Does the partial fractions technique work only for rational functions?
But yeah, my decomposition was wrong (now i see!)
But yeah, my decomposition was wrong (now i see!)
- #11
HallsofIvy
Science Advisor
Homework Helper
- 42,989
- 975
Since only rational functions are fractions, yes, partial fractions only works for rational functions!
1. What is a rational function integral?
A rational function integral is the process of finding the antiderivative of a rational function, which is a function that can be expressed as the quotient of two polynomials. It is a type of indefinite integral and is often used in calculus to solve problems related to areas and volumes.
2. How do you solve a rational function integral?
To solve a rational function integral, you can use a variety of techniques such as substitution, integration by parts, or partial fractions. The specific method used will depend on the complexity of the rational function and the tools available. It is important to follow the rules of integration and to simplify the expression as much as possible before attempting to integrate.
3. Are there any special cases when integrating rational functions?
Yes, there are a few special cases when integrating rational functions. One is when the degree of the numerator is greater than or equal to the degree of the denominator, in which case the integral will involve a polynomial division. Another case is when the rational function contains a quadratic expression in the denominator, which may require the use of trigonometric substitutions. Additionally, if the rational function has any terms involving square roots, it may be necessary to use a u-substitution.
4. What are some real-life applications of rational function integrals?
Rational function integrals have many real-life applications, particularly in the field of physics. They can be used to calculate the work done by a variable force, the center of mass of an object, and the volume of a solid of revolution. In engineering, rational function integrals are used to find the moment of inertia of an object and the deflection of a beam under load. They are also useful in economics for calculating marginal cost and marginal revenue.
5. Are there any common mistakes to avoid when integrating rational functions?
Yes, there are a few common mistakes that should be avoided when integrating rational functions. These include forgetting to use the proper rules of integration, not simplifying the expression before integrating, and incorrectly setting up the integral by forgetting to include all terms. It is also important to check for any potential discontinuities or vertical asymptotes in the rational function before integrating. Additionally, it is always a good idea to double-check your answer by differentiating it to ensure it is correct.
Similar threads
- Replies
- 3
- Views
- 1K
-
Calculus
- Replies
- 4
- Views
- 839
- Replies
- 11
- Views
- 160
- Replies
- 4
- Views
- 910
- Replies
- 8
- Views
- 176
- Replies
- 31
- Views
- 924
-
Calculus
- Replies
- 5
- Views
- 2K
-
Calculus
- Replies
- 3
- Views
- 1K
-
Calculus
- Replies
- 8
- Views
- 1K
- Replies
- 8
- Views
- 425
Share: