Rayleigh-Ritz Method and Distributed Parameter Systems

[Whitebread]

Homework Statement

Let me begin by saying that this will be a long post and will involve a few homework questions. I'm not looking for answers for per-say. Instead, I am looking to deepen my vague understanding of the Rayleigh-Ritz Method and how one can use it to find the mode shapes and natural frequencies of distributed and lumped parameter systems. Also note that I have already attempted to utilize my professor and TA as resources, but I've had other, more pressing issues to take up with my professor and my TA is just atrocious.

Anyway, the homework in question is as follows:

1a) For the figure given, cantilevered beam with a tip find the exact eigenvalues and eigenfunctions for the system. (graduate student required, extra credit for undergraduates).

1b) Using the Rayleigh-Ritz method, compare and approximate solution of the following beam problem to a close form beam solution (part 1a) (undergraduates choosing not to do the extra credit, could compare to a cantilevered beam, with no tip mass). Compare natural frequencies (in Hertz) and mode shapes for each system.

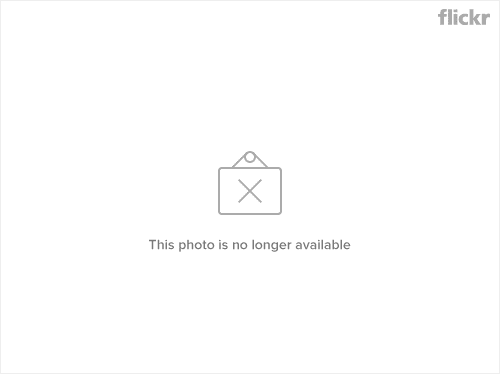
Use the mode shape of a cantilevered beam in your Ritz method.


2) Using the Rayleaigh-Ritz method predict the eigenvalues and mode shapes for the following system.

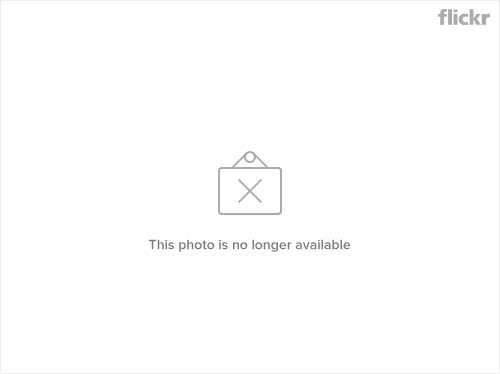
Compare the eigenvalues of the system for kL/EI = .1, 1, 10; assume a four function expansion. Discuss how the solution changes for the system with increasing spring constant. Tabulate the natural frequencies for the beam alone, and for the beam/spring system.

The very first question (1a) I believe I can solve without problem. I've never had to find the natural frequencies and mode shapes in transverse vibration for a bean with a point mass at the end, but I have done so with longitudinal vibrations. In a like manner, I'm assuming that the Euler-Bernoulli beam equation can be used with an adjustment to the boundary conditions.

1b and 2 are the questions I cannot solve. I'm not explicitly looking for solutions, as I'd like to do and learn them myself. I would, though, really appreciate a thorough explanation of the following example problem (see the next section), or a similar example problem lifted from some other text.

Homework Equations

The example problem I have been given is attached.

The Attempt at a Solution

I have a basic understanding of the Rayleigh-Ritz Method, but I do not understand how to apply it to the attached questions, nor do I understand the attached example. Again, all I'm looking for is an explanation of the example, or similar problem, so that I can finish the last 2 homework questions. I've read a few technical writings concerning the Rayleigh-Ritz method, but none deal explicitly wit this subject. There are about 250 different books in my schools library that deals with this variational method, in one way or another, but I don't have time to inspect them all. I figured this website would hasten my search.

Thanks guys.

 

[KataKoniK]

Thank you for reaching out for help with your homework questions. The Rayleigh-Ritz method is a powerful tool for solving problems involving distributed and lumped parameter systems, and I am happy to help deepen your understanding of it.

For the first question (1a), you are correct in thinking that the Euler-Bernoulli beam equation can be used with an adjustment to the boundary conditions. The specific boundary conditions for a cantilevered beam with a point mass at the end are:

- The displacement at the fixed end (x = 0) is zero: u(0) = 0
- The bending moment at the fixed end is zero: M(0) = 0
- The shear force at the fixed end is equal to the point mass: V(0) = mω²

To solve this problem, you can use the general solution to the Euler-Bernoulli beam equation:

u(x) = A sin(αx) + B cos(αx) + C sinh(αx) + D cosh(αx)

Where A, B, C, and D are constants to be determined, and α is the eigenvalue.

Applying the boundary conditions, we get:

u(0) = 0 -> B + D = 0
M(0) = 0 -> Aα - Cα = 0
V(0) = mω² -> Bα + Dα = mω²

Solving for the constants, we get:

A = 0
B = -mω²/α
C = 0
D = mω²/α

Therefore, the displacement function for the cantilevered beam with a point mass at the end is:

u(x) = -mω²/α cos(αx) + mω²/α cosh(αx)

The corresponding natural frequency is ω = √(α/EI).

For part 1b, you are asked to compare this exact solution to an approximate solution using the Rayleigh-Ritz method. The Rayleigh-Ritz method involves approximating the displacement function with a trial function that satisfies the boundary conditions. In this case, we can use the mode shape of a cantilevered beam (without the point mass) as our trial function. This means that our trial function is:

u(x) = A sin(αx)

Applying