VinnyCee
- 486
- 0
Homework Statement
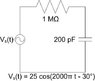
I can't post pictures as I do normally, so you'll have to deal with the cumbersome attachment method! It's just a simple RC circuit. Resistor on top, capacitor on right side with the sinusoidally varying voltage source on the left.
V_s(t)\,=\,25\,cos\left(2000\,\pi\,t\,-\,30^{\circ}\right)
Obtain an expression for v_c(t), the voltage across the capacitor.
NOTE: Picture of circuit is attached.
Homework Equations
A\,cos\left(\omega\,t\,+\,\phi_0\right)\,\,\longrightarrow\,\,A\,e^{j\,\phi_0}
j\,=\,e^{j\,\frac{\pi}{2}}
Various equations and conversions from the text, Fundamentals of Applied Electromagnetics (Ulaby, 5 ed.) PROBLEM 1.21
The Attempt at a Solution
I obtained the voltage equation for the RC circuit as:
R\,i(t)\,+\,\frac{1}{C}\,\int\,i(t)\,dt\,=\,v_s\,(t)
Now, I convert to phasor form:
R\,\tilde{I}\,+\,\frac{1}{C}\,\left(\frac{1}{j\,\omega}\,\tilde{I}\right)\,=\,V_s
The book gives a conversion to get the phasor expression for the current:
\tilde{I}\,=\,V_0\,e^{j\,\left(\phi_0\right)}\,\frac{j\,\omega\,C}{j\,\omega\,C\,R\,+\,1}
I apply this formula, given for the RC circuit by the text, and I get this:
\tilde{I}\,=\,25\,e^{-j\,30^\circ}\,\frac{j\,\left(2000\,\pi\right)\,\left(200\,X\,10^{-12}\right)}{j\,\left(2000\,\pi\right)\,\left(200\,X\,10^{-12}\right)\,left(1\,X\,10^6\right)\,+\,1}
\tilde{I}\,=\,25\,e^{-j\,30^\circ}\,\frac{j\,4\,X\,10^{-7}\,\pi}{j\,0.4\,+\,1}
Then, after doing some manipulation of the complex number:
\tilde{I}\,=\,0.0000229\,+\,j\,0.0000180\,=\,2.29\,X\,10^{-5}\,+\,j\,1.8\,X\,10^{-5}
I know that this is probably not correct, but I went ahead and used it in the subsequent equation (also given in the text) to find the capacitor voltage phasor:
\tilde{V_c}\,=\,\frac{\tilde{I}}{j\,\omega\,C}
After some plug & chug…
\tilde{V_c}\,=\,14.3\,-\,j\,18.2
This is NOT the answer given in the text! I know I didn't convert back from phasor form, but still... The correct answer is:
V_c(t)\,=\,15.57\,cos\left(2000\,\pi\,t\,-\,81.5^{\circ}\right)
Where did I go wrong? Can anyone get me started on the right track here?
Attachments
Last edited: