paddu123
- 2
- 0
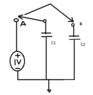
For the attached rc circuit, at time 0, the switch switches from A to B, how to figure out the voltage wave form at B?
When switch switches from A to B, charge has to redistribute between capacitors, but as the voltage across capacitor C2 can't change instantaneously initially there is a spark and charge distributes slowly. Please help me if this is right to interpret or not?
When switch switches from A to B, charge has to redistribute between capacitors, but as the voltage across capacitor C2 can't change instantaneously initially there is a spark and charge distributes slowly. Please help me if this is right to interpret or not?