Reaction force on a leaned beam

[Karol]

Homework Statement

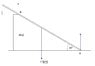
A beam of 12[kN] is on a smooth floor on one side and on a rough edge on the other.
The total length of the beam is 10[m].
What is the reaction on the edge.

Homework Equations

Moments (torque): F₁L₁=F₂L₂

The Attempt at a Solution

I drew the forces. the reaction on the floor is vertical and also on the edge since there aren't horizontal forces.
Moments around point A:
$$12[kN]\cdot 5\cdot \cos 30^0=R\cdot\frac{4[m]}{\tan 30^0}\rightarrow R=7.5[kN]$$
In the book it's 6.5, i think it's a mistake

 

[haruspex]

I agree with 7.5kN.

Edit: looks like they took the horizontal distance for mg but the distance up the slope for the wall's reaction.
Edit 2: ... are you sure they wanted the total reaction, not just the normal reaction from the wall?

 

[Karol]

I am almost sure they want the total reaction.
I leave this problem since i have another one, a little more problematic