Real World Trig Problem - Thanks in Advance

[txglassguy]

I work for a glass replacement company where we replace broken glass in highrise buildings.

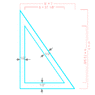
My question is this, I have a piece of glass that we call a rake, but is really just in the shape of a right angle. The measurement from inside the building, called the daylite measurement, is 37 1/8" at the base, 73 5/8" for the heigth, and the hypotenuse is 82 1/2".

In order to turn the daylite measurement into a glass size, 1" needs to be added to the measurement (basically draw a triangle outside the original that is 1/2" bigger all the way around).

What is the best and easiest way to calculate this problem? I read several posts on sin and cos, but could not put it all together (not to mention it has been 15 years since I took trig...).

Thanks in advance for your help.

 

[DaveC426913]

Visual aid.

Solve for b' and h'.

It's not as easy as I thought at first.

 

[txglassguy]

Thanks for adding the pic, it is exactly as I would have drawn it. How did you add it so that I know for next time?

 

[DaveC426913]

1] 'Go Advanced'
2] Select the little paperclip icon from the features.

 

[DaveC426913]

The key to your problem will be to draw construction lines onto the diagram, dividing up the areas in the upper left and lower right until you have smaller, simple shapes (triangles and possibly one parallelogram) whose dimensions you know or can derive.

 

[Integral]

Easy in Auto Cad, Offest each side .5", extend,trim, measure.

 

[DaveC426913]

Another solution would be to skip the numeric solution altogether and simply do an analogue solution (i.e draw it in Photoshop at a suitable size and measure it). How accurate do you need it to be in fractions of an inch?

 

[txglassguy]

Judging by glass that we have had in the past that we could actually measure the broken piece in its entirety, the new base and heighth had about over an inch added to them in order to create the correct hypotenuse. Needs to be acurate down to +-1/16"

Also, I would love to have CAD, but all I have is a calculator...

 

[txglassguy]

It seems as if I drew smaller triangles using .5" for the base of one and .5" for the heigth of the other that I could find the corresponding heigth and base. How do I find the angles and what trig formula would I use?

 

[DaveC426913]

I get
37 15/16"
75 3/4"
84 3/4"

You can see that the new piece is 13/16" wider at the base and 2 1/8" taller.

 

[DaveC426913]

It seems as if I drew smaller triangles using .5" for the base of one and .5" for the heigth of the other that I could find the corresponding heigth and base. How do I find the angles and what trig formula would I use?

That won't work.

 

[txglassguy]

So you got that solution out of photoshop? Those numbers look right.

 

[DaveC426913]

So you got that solution out of photoshop? Those numbers look right.

Yes, I drew it up at .01inch/pixel. Once I got the measurements, I cross-checked them by comparing the old slope and new slope.

 

[Integral]

Dave,
Something is wrong, your results do not pass the obvious check. Each side MUST be at least 1" longer then the original.
Here is a analytic solution


Here is a bigger version on photobucket

http://i220.photobucket.com/albums/dd24/Integral50/TRIANGLE1.jpg"

 

[txglassguy]

What is the solution if you plug it into cad?

 

[Integral]

Unfortunately I am at home, Auto Cad is at work.

I would suggest cutting a real sized template in cardboard using the dimensions I computed. Dave's cannot be right, and I have a high confidence in my algebra.

 

[Redbelly98]

I independently get the same answer as Integral.

New base = 38.44" or 38-7/16"
New height = 76.23" or 76-7/32"

p.s. I get 63.24 degrees for the base angle, and 26.76 degrees for the top angle.

p.p.s. This is from an analytic solution, i.e. not CAD.

 

[maze]

I get redbellys answer, using similar triangles. Here is a diagram:
http://img236.imageshack.us/img236/2198/similartriswindowkx6.png

 

[DaveC426913]

Yes, my answer is wrong. (Though I don't know where I went wrong.)