akaf244
- 2
- 0
- TL;DR Summary
- rectified current through inductor
Hello, I need to find the magnetomotive force (mmf) of an inductor using NI (turns multiplied by amperes). The set up is pretty simple, AC power supply set at 24 VAC goes through a full wave rectifier (4 diodes) and into an inductor. If the inductor has a resistance of 47 Ohms, it looks like this (ignore Ls and Rs)...
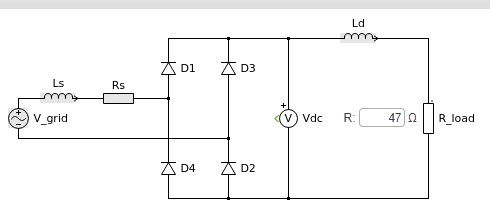
I have spent a few hours and a lot of different equations trying to figure out the current flowing through the inductor. I know it will look something like this...
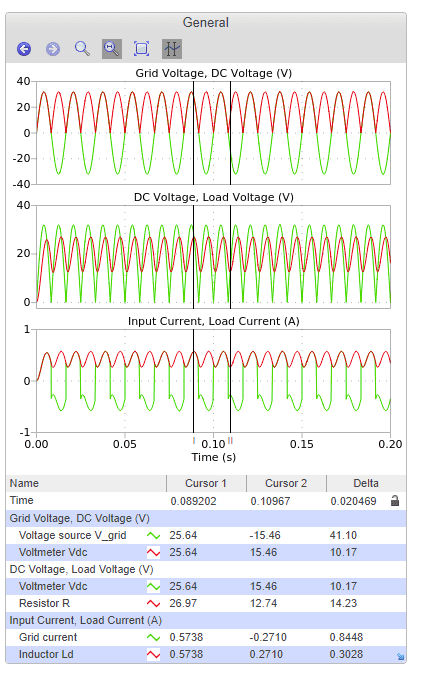
but can anyone explain to me how they are graphing the current??
Thank you! (screenshots from: https://www.plexim.com/academy/power-electronics/diode-rect-ind-load )
I have spent a few hours and a lot of different equations trying to figure out the current flowing through the inductor. I know it will look something like this...
but can anyone explain to me how they are graphing the current??
Thank you! (screenshots from: https://www.plexim.com/academy/power-electronics/diode-rect-ind-load )