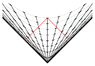
Here's my favorite example:
The text in
http://www.astro.ucla.edu/~wright/cosmo_02.htm
associated with the attached image evaluates a special case where both the standard SR distances and velocities and the cosmoloigcal distances (comoving distance) and velocities (Hubble velocity) are defined.
More advanced readers might recognize this as the "Milne" cosmology, other less advanced readers may not recognize it from this description - Ned Wright doesn't use this particular phrase in his text.
The point of this image though is to point out that the cosmologists are measuring something that's different from the standard SR notion of distance and velocity. This can be seen by this specific example, which applies to a cosmology where both concepts exist.
The SR notions of distance and velocity cannot, unfortunately, be generalized to situations where the Riemann tensor is non-zero (i.e. the spacetime is curved). SR notions of distance and velocity require a Minkowskian metric. The example was specifically chosen so that the space-time in question has both a Minkowskian metric (a static flat space-time description) and a Milne metric (a non-static expanding space-time description) which are mathematically totally equivalent, representing the same physical spacetime (a spacetime with a very low matter density).
The cosmological defintions of distance and velocity are more general than the SR defintions, but they do
NOT reduce to the SR defintions of distance and velocity in this limit of low matter density.
As I went on at some length in another thread, the important point here is "many distances, many velocities". One should be aware that the definitions of distance (of which there are many) used by cosmologists are not the same as those used in SR, and that this remark also applies to velocities (though in this case only the Hubble recessional velocity is widely used AFAIK).
This should not be terribly surprising to someone who is familiar with SR - one of the reasons for this difference in defintions is the usual problems of defining "simultaneous" events, which is a necessary prerequisite to be able to measure distance.