- #1
DavidAp
- 44
- 0
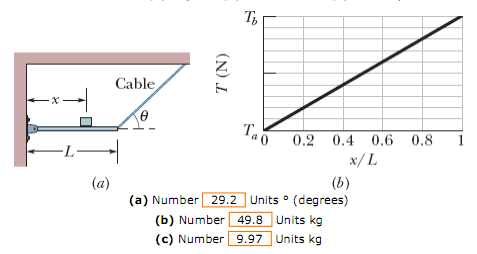
Figure 12-52a shows a horizontal uniform beam of mass mb and length L that is supported on the left by a hinge attached to a wall and on the right by a cable at angle θ with the horizontal. A package of mass mp is positioned on the beam at a distance x from the left end. The total mass is mb + mp = 59.8 kg. Figure 12-52b gives the tension T in the cable as a function of the package's position given as a fraction x/L of the beam length. The scale of the T axis is set by Ta 500 N and Tb 700 N. Evaluate (a) angle θ, (b) mass mb, and (c) mass mp.
The answers are displayed at the bottom of the diagrams.
Related Equation:
T = r*Fτ
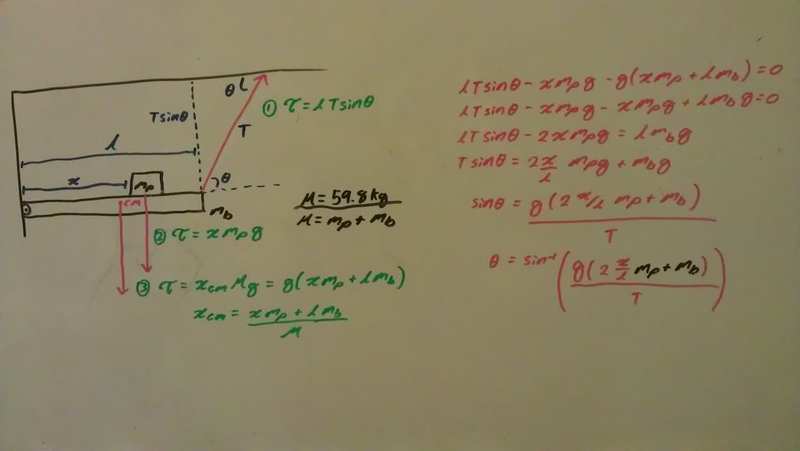
My attempt at this problem can be seen in the image below. I decided to write it on my board to make it easier to follow and less strenuous on the eyes; however, if my handwriting is illegible please do not hesitate to tell me for I will retype it for you as a response. Although my work below doesn't show it I have been tackling this problem for over an hour on various sheets of paper and have been able to get no where so any help is much appreciated.
I feel as if I am suppose to isolate mp+mb so that I may replace it with M but in my final equation I am unable to due so because 2x/l is being multiplied to mp. As for x/l and T, if I am able to isolate mp+mb, I was just planning on picking a random point on the chart above to place into my equation. Is this what I'm suppose to do?
Thank You for taking the time to review my question.
(note) I'm sorry if the size of my image creates any inconveniences.
(edit) Small grammer mistakes.
The answers are displayed at the bottom of the diagrams.
Related Equation:
T = r*Fτ
My attempt at this problem can be seen in the image below. I decided to write it on my board to make it easier to follow and less strenuous on the eyes; however, if my handwriting is illegible please do not hesitate to tell me for I will retype it for you as a response. Although my work below doesn't show it I have been tackling this problem for over an hour on various sheets of paper and have been able to get no where so any help is much appreciated.
I feel as if I am suppose to isolate mp+mb so that I may replace it with M but in my final equation I am unable to due so because 2x/l is being multiplied to mp. As for x/l and T, if I am able to isolate mp+mb, I was just planning on picking a random point on the chart above to place into my equation. Is this what I'm suppose to do?
Thank You for taking the time to review my question.
(note) I'm sorry if the size of my image creates any inconveniences.
(edit) Small grammer mistakes.
Last edited: