Relation between "widths" of non-paralleogram

[julian]

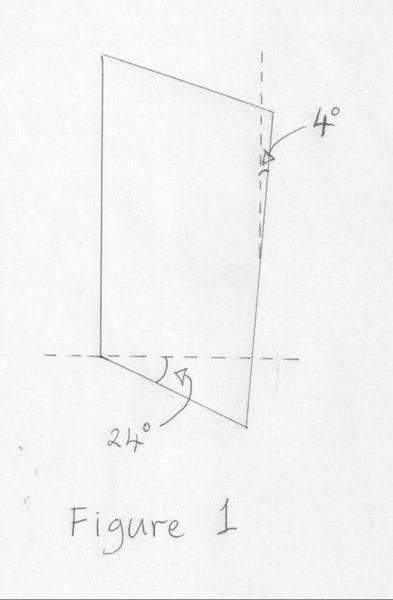
I'm trying to relate different ways of getting a value for the "width" of a non-parallelogram. The non-parallelogram is given in figure 1: note that the left-hand side edge is vertical, the right-hand side is tilted 4 degrees away from vertical, and the bottom edge is 24 degrees below the horizontal.

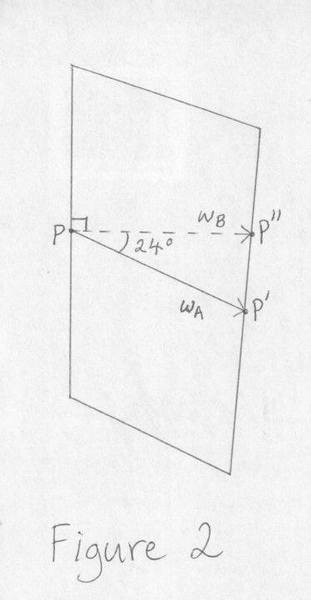
(i) One way of obtaining a value for the "width" is measuring the distance between the two sides midway up while having the ruler parallel to the bottom edge. This is represented by the solid line with arrow in figure 2 from point $P$ to point $P'$. We label the value this distance by $w_A$.

(ii) Another way would be to measure the distance but having the ruler horizontal (that is, have the ruler at right-angles to the left-hand side edge). This is represented by the dashed line with arrow in figure 2 from point $P$ to point $P''$. We label this distance by $w_B$.

(iii) Another way would be to find the least distance from the point P to the right-hand side edge. We label this distance by $w_C$.

Note that for a perfect rectangle we would have $w_A = w_B = w_C$!

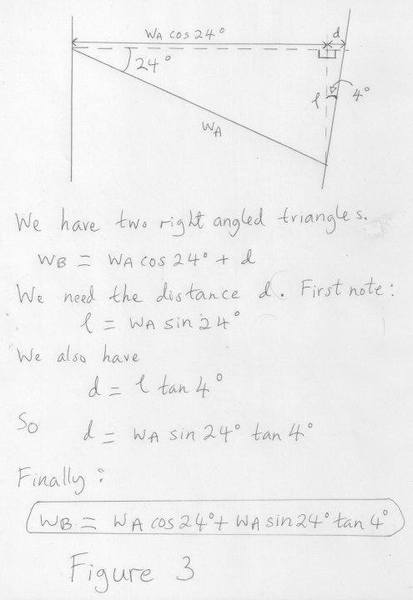
Figure 3 is a close up of the triangle $PP'P''$ from figure 2. Obviously this is a non-right-angled triangle but can be split into two right angled triangles. From this I can relate $w_B$ to $w_A$:

$w_B = w_A \cos 24^0 + w_A \sin 24^0 \; \tan 4^0$

(see figure 3 for calculation). Is that correct?

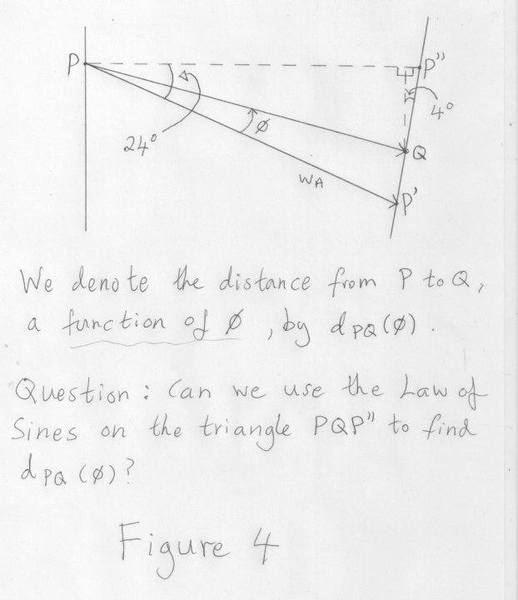
In order to address part (iii) I want to find a formula for the distance from the point $P$ to the point $Q$ as a function of $\phi$ as indicated in figure 4. Wondering if I could use the Law of Sines on the triangle $PQP''$ in figure 4 to do this and how to go about it? I could then use simple calculus to find minimum or/and plot the function on wolfram given $w_A = 5.1$.

 

[HallsofIvy]

You don't need "to find a formula for the distance from the point P P to the point Q Q as a function of ϕ as indicated in figure 4." It is easy to show that the shortest distance from a point to a line is along a perpendicular to that line and that is what you already have.

 

[julian]

You don't need "to find a formula for the distance from the point P P to the point Q Q as a function of ϕ as indicated in figure 4." It is easy to show that the shortest distance from a point to a line is along a perpendicular to that line and that is what you already have.

I want the least distance from the point P to the right-hand edge. The right-hand edge is tilted away from vertical by 4 degrees, so a line from P will meet the right-hand edge perpendicularly if this line is 4 degrees below the horizontal. Correct?

The least distance from the point P to the right-hand edge will be then be $w_B \cos 4^0$, or

$(w_A \cos 24^0 + w_A sin 24^0 \; \tan4^0) cos 4^0$

Substituting in $w_A = 5.1$, we get the minimum distance is 4.79.

(Important to note that the line $PP''$ does not meet the right-hand edge perpendicularly as the right-hand edge is tilted 4 degrees away from vertical - see figure 2).

(EDIT: meant to say the line $PP''$ - corrected it now.)

 

[julian]

I have been able to derive formula for $d_{PQ}$ using the law of sines on the triangle $PQP''$ - I will express it as a function of $\phi$ where THIS TIME $\phi$ is defined as the angle below the horizontal:

$d_{PQ} (\phi) = {w_A cos 24^0 + w_A \sin 24^0 \tan 4^0 \over \cos (4^0 - \phi)}$

I put $w_a = 5.1$ and plotted the function on wolfram:

http://www.wolframalpha.com/input/?.../+cos+((4+-+\phi)+*+pi/180))+between+0+and+24

and there is indeed a minimum at $4^0$, with the minimum distance is 4.79!

(Note: that wolfram calculates in radians, but I want to work in degrees - this is easily taken care of by multiplying every angle by $\pi / 180$).

 

[julian]

You don't need "to find a formula for the distance from the point P P to the point Q Q as a function of ϕ as indicated in figure 4." It is easy to show that the shortest distance from a point to a line is along a perpendicular to that line and that is what you already have.

I see. You are in actual fact answering the question what is the least distance from the point $P''$ to the left-hand edge (line), and $w_B$ would indeed be the answer (see from figure 2 that the dashed line from $P''$ to $P$ is perpendicular to the left-hand edge).

However, what I asked was what is the least distance from the point $P$ to the right-hand edge (line). These two questions have different answers precisely because it is a non-parallelogram. Whence the factor $\cos 4^0$ in $w_B \cos 4^0$.

 

[julian]

So I want the least distance from the point $P$ to a line, the line being the right-hand edge. I've drawn a diagram to clarify the situation - see figure "least".

Note the horizontal (the dashed line) is NOT perpendicular to the right-hand edge because the right-hand edge is tilted away from vertical by $4$ degrees.

I have drawn in the perpendicular to the right-hand edge. It shouldn't be too difficult to see that the length of the perpendicular is $w_B \cos 4^0$, where $w_B$ is the length of the horizontal - see figure "least".