Quentin_Phys
- 1
- 2
I would like to ask a question on whether there is a proportionality between volume of a balloon, and the time it takes to deflate.
I have conducted several balloon hovercraft experiments. I need to find the relationship between the amount of air pumped into the balloon and how long the hovercraft hovers. The balloon is tied on a sport bottle cap, with an acrylic disc as its base. The cap is glued onto the disc.
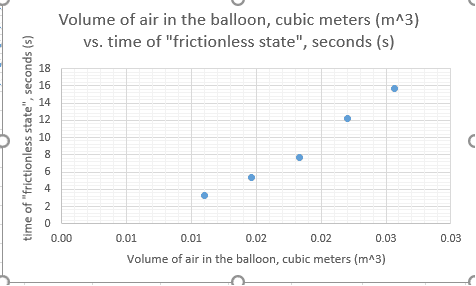
I have plotted such a graph, with volume on the x-axis and time of flight on the other. I have achievement a seemingly exponential trend. I would like to know if there is a formula that can find my proportionality of the relationship between volume and how long the it takes for the balloon to deflate (the hovercraft to float).
Thank you.
Here is a sample of the theoretical data:
I have conducted several balloon hovercraft experiments. I need to find the relationship between the amount of air pumped into the balloon and how long the hovercraft hovers. The balloon is tied on a sport bottle cap, with an acrylic disc as its base. The cap is glued onto the disc.
I have plotted such a graph, with volume on the x-axis and time of flight on the other. I have achievement a seemingly exponential trend. I would like to know if there is a formula that can find my proportionality of the relationship between volume and how long the it takes for the balloon to deflate (the hovercraft to float).
Thank you.
Here is a sample of the theoretical data:
Last edited: