bkw2694
- 33
- 0
Homework Statement
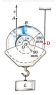
As shown in the picture, two pulleys are riveted together with a known velocity. I need to find the velocity of two other points.
Homework Equations
V_A = VB + <ω> x <BA>
V = ωr
The Attempt at a Solution
I've honestly been trying to figure this one out for over a week, and I'm sure I'll kick myself when I realize how easy it is, but I'm trying to solve by:
V_A = (r_OA)*(ω_OA), using V_A = .9 m/s; r_OA = 90mm, which gives me ω_OA = 10 rad/sec (which I assume ω is equal on the entire pulley since it's riveted together).
Then I used the relative velocity vector formula for A and O:
V_A = V_O + <-10 rad/sec k> x <-.09 m i>
which gives me: .9 m/s j = V_O j + .9 m/s j. Solving with this gives me V_O = 0, which is incorrect. I tried solving for B the same way.
The actual answers are V_O = .6 m/s, and V_B = .849 m/s.
Thanks in advance!