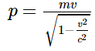Relativistic calculation of speed when the momentum is known

[Karagoz]

Homework Statement

We know the momentum of an electron, which is: 1,48*10^-21.

Momentum is m*v (mass*speed)

If we divide the momentum by the mass of the electron to find electron's speed, it'll give a value where v> 3*10^8 m/s.

Since speed can't be above speed of light, we have to calculate it relativistic to find the speed of light of the electron.

Homework Equations

gives:

The Attempt at a Solution

With the formula above, the problem is easy to solve.

But I don't get how that formula is transformed.

When I try it, this is what I get:

p = mv/√(1 - v^2/c^2)

divide by m, and multiply by √(1 - v^2/c^2)

v = p/m * √(1 - v^2/c^2)

^2 both sides

v^2 = p^2/m^2 * (1 - v^2/c^2) = p^2/m^2 - (p^2*v^2)/(c^2*m^2)

making some changes so both have same divsor:

v^2 = (p^2*c^2)/(m^2*c^2) - (p^2*v^2)/(m^2*c^2)

How do they get the equation where:

v = (p*c) / √(p^2 + m^2*c^2)

??

 

[TSny]

v^2 = (p^2*c^2)/(m^2*c^2) - (p^2*v^2)/(m^2*c^2)

Collect together the terms that contain v² and factor out the v².
(The toolbar has a superscript tool.)

 

[Chandra Prayaga]

Start with your first Relevant equation and solve for v! Collect all the terms with v on one side, square everything to get rid of the square root, and solve for v²

 

[Orodruin]

We know the momentum of an electron, which is: 1,48*10^-21.

Also, remember that numbers are useless without appropriate units.

 

[Karagoz]

p = mv/√(1 - v^2/c^2)

p = mv/√(1 - v^2/c^2)

divide by m, and multiply by √(1 - v^2/c^2)

v = p/m * √(1 - v^2/c^2)

^2 both sides

v^2 = p^2/m^2 * (1 - v^2/c^2) = p^2/m^2 - (p^2*v^2)/(c^2*m^2)

making some changes on the right side so both have same divsor:

v^2 = (p^2*c^2)/(m^2*c^2) - (p^2*v^2)/(m^2*c^2)

This was where I left:

v^2 = (p^2*c^2)/(m^2*c^2) - (p^2*v^2)/(m^2*c^2)

Add + (p^2*v^2)/(m^2*c^2) on both sides.

v^2 + (p^2*v^2)/(m^2*c^2) = (p^2*c^2)/(m^2*c^2)

Get a common divisor on left side.

(v^2*m^2*c^2)/(m^2*c^2) + (p^2*v^2)/(m^2*c^2)

Simplify the left side

v^2(m^2*c^2 + p^2) / (m^2*c^2) = (p^2*c^2) / (m^2*c^2)

Multiply both sides by: (m^2*c^2)

v^2(m^2*c^2 + p^2) = (p^2*c^2)

divide by (m^2*c^2 + p^2)

v^2 = (p^2*c^2)/(m^2*c^2 + p^2)

SQROOT both sides:

v = (p*c) / √(m^2*c^2 + p^2)

v = (p*c) / √(p^2 + m^2*c^2)Do you know a more simplified way?

 

[Chandra Prayaga]

p/m = v / √(1 - v² / c²)
p² / m² = v² / (1 - v² / c²) = 1 / (1/v² - 1/c²)
(1/v² - 1/c²) = m² / p²
1/v² = (m² / p²) + (1/c²))
That separates the v to the left. Now take the lcm on the right hand side, invert, and take the square root.