Relativistic charged particle in a constant, uniform EM field

[Giuops]

Homework Statement

Find the four-momentum of a charged particle in an external, constant electric and magnetic field.

Relevant Equations

dpμ/dτ=q*Fμν*uν
pμ=muμ

I have to find pμ(τ) of a particle of mass m and charge q with v(0) = (vx(0), vy(0), vz(0)) in a electric field E parallel to the y-axis and a magnetic field B parallel to z axis, both constant and uniform, with E = B.

Here follows what I have done (see pictures below):

I wrote 4 differential equations (using that E=B) and called qE/m = a. The last equation (z axis) is immediately solved.

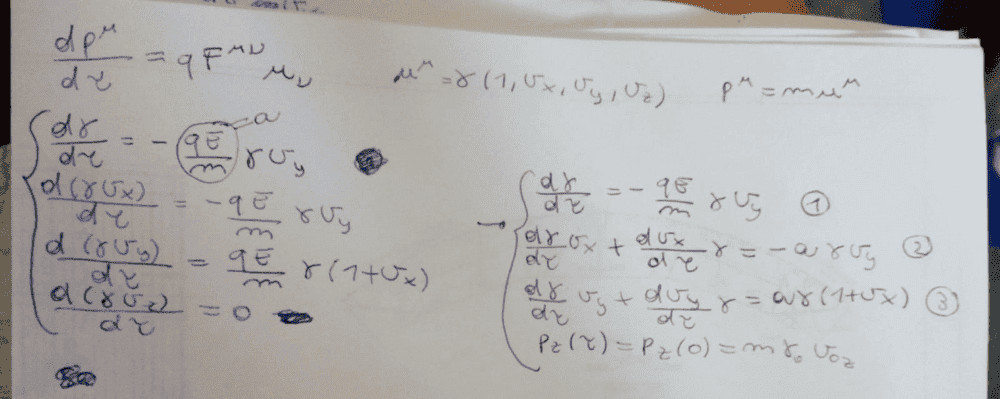
To solve the others, I substituted equation (1) in (2) and (3), obtaining this:

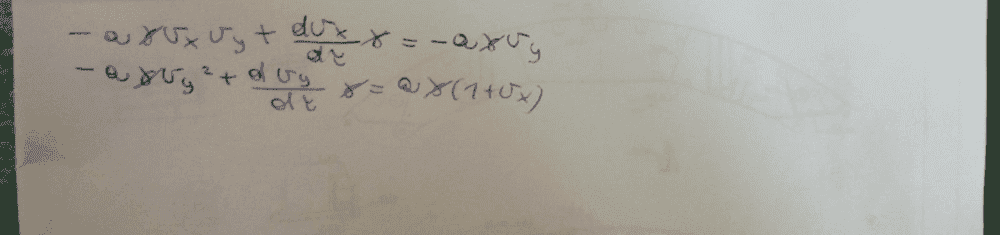
... but I don't know how to solve these. How do I find the x and y components of the four momentum?

Thanks for the read.

 

[timetraveller123]

ful disclosure i have seen this method online and not something i came up with myself

$\frac{d P^{\mu}}{d \tau} = q F^{\mu \beta}u_{\beta}\\$
i think $F^{\mu \beta}$ looks like this
$\begin{pmatrix} 0&0&E&0\\ 0&0&B&0\\ -E&-B&0&0\\ 0&0&0&0 \end{pmatrix}$
$m\frac{d^2 u^{\mu}}{d \tau^2} = q F^{\mu \beta} \frac{d u_{\beta}}{d \tau}\\ m\frac{d^2 u^{\mu}}{d \tau^2} = \frac{q}{m} F^{\mu \beta} \frac{d P_{\beta}}{d \tau}\\ m\frac{d^2 u^{\mu}}{d \tau^2} = \frac{q^2}{m} F^{\mu \beta} F_{\beta \alpha}u^{\alpha}\\ F^{\mu \beta} F_{\beta \alpha} = \begin{pmatrix} E^2&-EB&E&0\\ -EB&-B^2&B&0\\ 0&0&E^2-B^2&0\\ 0&0&0&0 \end{pmatrix}$
this has uncoupled the $u^y$ equation and since$E^2 - B^2 = 0$ it is quite easy to solve for it and then you plug $u^y$ into earlier equations to get other components
someone tell me if it is wrong

 

[TSny]

$F^{\mu \beta} F_{\beta \alpha} = \begin{pmatrix} E^2&-EB&E&0\\ -EB&-B^2&B&0\\ 0&0&E^2-B^2&0\\ 0&0&0&0 \end{pmatrix}$

Looks like there are some "typos" here. We can let @Giuops find them if he/she wants to.

This way of uncoupling the equations is pretty nifty.

 

[timetraveller123]

Looks like there are some "typos" here.

oh i think i see them i think forgot to change some values after copying the first matrix