AlMetis
- 98
- 7
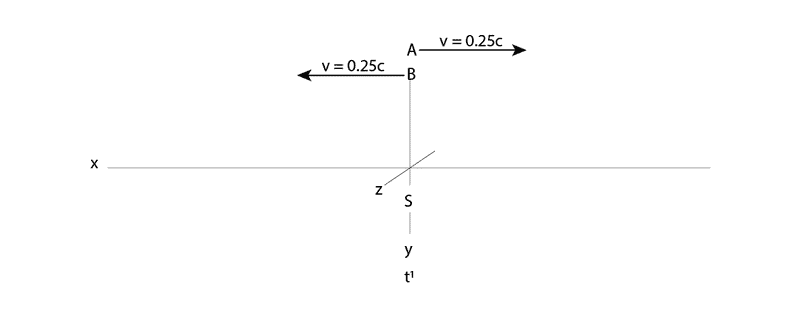
A frame “A” of three perpendicular axis (x, y, z) and an identical frame “B”, with an observer at rest in each, are moving toward each other at 1/2c on their common x axis.
Centered between A and B on x is a light source S.
At the time t1 when A, B and S coincide on x, S emits a light flash.
Given the symmetry of motion between A, B and S, are the paths observed by A and B a mirror of each other?
If not, please explain.

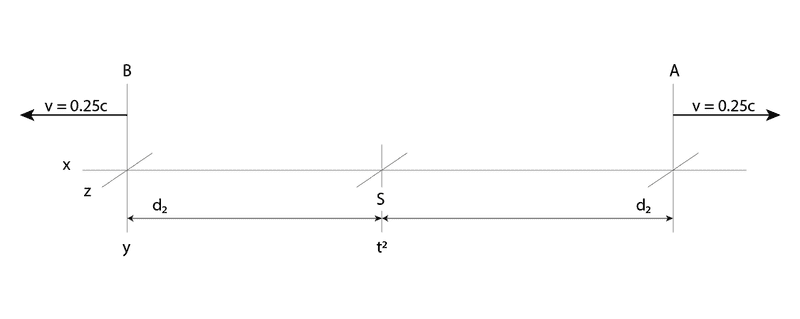
Centered between A and B on x is a light source S.
At the time t1 when A, B and S coincide on x, S emits a light flash.
Given the symmetry of motion between A, B and S, are the paths observed by A and B a mirror of each other?
If not, please explain.