Res-Monster Maze: Find Current Through R

[STEMucator]

Homework Statement

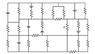
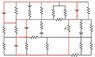
Res-monster maze. In the following figure, all the resistors have a resistance of $4.0 \Omega$ and all the (ideal) batteries have an emf of $4.0 V$. What is the current through resistor $R$?

Homework Equations

$\sum V = 0$
$\sum I = 0$
$V = \epsilon$
$V = IR$

The Attempt at a Solution

See the attached image.

When I look at it, I see two loops. The big loop to the left of $R$ and the smaller loop to the right of it. Would I just apply the equations in that sense?

Left loop:

$\epsilon_1 - i_1R - i_2R' - i_3R'' = 0$

Right loop:

$\epsilon_2 - i_4R''' + i_5R = 0$

EDIT: Wait what if I just find an equivalent resistance for that one standout parallel resistor combination?

 

[NascentOxygen]

The easy way is to see whether there exists a string of nothing but pure voltage sources between one end of R and its other end. Any other method will be many orders of magnitude more complicated.

You know how to play snakes-and-ladders, right?

 

[STEMucator]

The easy way is to see whether there exists a string of nothing but pure voltage sources between one end of R and its other end. Any other method will be many orders of magnitude more complicated.

You know how to play snakes-and-ladders, right?

I attached a picture of what I think you mean.

Writing the loop equation now:

$iR + \epsilon_1 - \epsilon_2 - \epsilon_3 - \epsilon_4 = 0$
$i = \frac{- \epsilon_1 + \epsilon_2 + \epsilon_3 + \epsilon_4}{R}$
$i = \frac{8.0 V}{4.0 \Omega}$
$i = 2 A$

 

[NascentOxygen]

I attached a picture of what I think you mean.

Writing the loop equation now:

$iR + \epsilon_1 - \epsilon_2 - \epsilon_3 - \epsilon_4 = 0$
$i = \frac{- \epsilon_1 + \epsilon_2 + \epsilon_3 + \epsilon_4}{R}$
$i = \frac{8.0 V}{4.0 \Omega}$
$i = 2 A$

That looks right.

 

[HalfLostAndSearching]

I would first clarify the question and make sure I understand what is being asked. It seems that the question is asking for the current through resistor R, but it is not specified which direction the current is flowing. I would ask for clarification on this point.

Assuming that the current is flowing clockwise in the circuit, I would approach this problem by first finding the equivalent resistance of the parallel combination of resistors R and R''. This can be done using the formula $R_{eq} = \frac{R_1R_2}{R_1+R_2}$. In this case, $R_{eq} = \frac{4 \times 4}{4+4} = 2 \Omega$.

Next, I would use Kirchhoff's laws to set up equations for the two loops, as the attempt at a solution suggests. I would then solve the equations simultaneously to find the currents in each loop. Since the current through resistor R is the same in both loops, this will give us the current through resistor R.

Alternatively, I could also use Ohm's law to find the current through resistor R directly, by using the equivalent resistance of the parallel combination and the voltage across it. In this case, $I = \frac{V}{R} = \frac{4V}{2 \Omega} = 2A$. Therefore, the current through resistor R is 2A.