- #1
Richard92
- 2
- 0
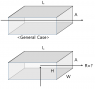
As you know, resistance of a rectangular shape is given by R=ρ A/L
But how do we theoretically calculate the resistance of the bottom case? ( now, the current flow is not parrallel, current flows from bottom through the right side)
I would like to know if there is any references for this calculation,
As far, I found a reference on EDN forum, (http://www.edn.com/design/component...thod-to-quickly-estimate-PWB-trace-resistance)
Jaeger has experimentally calculated on a case which the current flows on right angle. (resistance drops by 0.56 *(sheet resistance) )
But how do we theoretically calculate the resistance of the bottom case? ( now, the current flow is not parrallel, current flows from bottom through the right side)
I would like to know if there is any references for this calculation,
As far, I found a reference on EDN forum, (http://www.edn.com/design/component...thod-to-quickly-estimate-PWB-trace-resistance)
Jaeger has experimentally calculated on a case which the current flows on right angle. (resistance drops by 0.56 *(sheet resistance) )