Resistance, current and current density

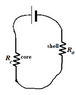
[Schfra]

Homework Statement

A coaxial cable consists of a core cylindrical wire and a coaxial cylindrical shell, as illustrated in the Figure below. Consider a cable made of copper, which has resistivity of
ρ=1.70×10−8Ω·m. Thecorewirehasaradiusof r =1.0mm. Theinnerradiusofthe 1
outer shell is r = 5.0 mm, and the outer radius of the shell is r = 6.0 mm. The length of 23
the cable is L = 1.5 m. The electron number density in the material of the wire is n = 2.0×1022 1/m3. A battery with electromotive force of E = 1.50 V is connected
between the core and shell of the cable at one end, while at the other end a resistance-less wire connects the core and shell of the cable. Hint: Beware of unit conversion!

a. (6) What is the resistance Rc of the core wire? And what is the resistance Rs of the
outer shell?
b. (6) What is the current I through the core wire?
c. (4) The current density J is uniform in the conductors. What is its magnitude in the
core wire and in the shell?

This is just for practice, I have the answer key. I understand a but I’m not quite sure I totally understand the next two parts.

Homework Equations

V = IR

J = I/A

The Attempt at a Solution

[/B]
For a, Rc = 8.12E-3
Ra = .74E-3

For b.) V = IR
1.5 = I(Rc + Ra)
= 170

I don’t have a clear understanding of why the resistance is the sum of the resistances of both wires here? Are they somehow in series? If so, why?

And for part c I have a similar question. What is the area being used in the calculation and why?

 

[TSny]

I don’t have a clear understanding of why the resistance is the sum of the resistances of both wires here? Are they somehow in series? If so, why?

Trace the path of the current from the positive terminal of the battery through the cable until you get to the negative terminal of the battery.

And for part c I have a similar question. What is the area being used in the calculation and why?

No calculation is shown for part (c). Describe in words the shape of the area that you are interested in. If you are not sure, review the definition of current density.

 

[Schfra]

Trace the path of the current from the positive terminal of the battery through the cable until you get to the negative terminal of the battery.

No calculation is shown for part (c). Describe in words the shape of the area that you are interested in. If you are not sure, review the definition of current density.

Here’s a picture of the diagram. The reason I’m confused is because of the odd placement of the resistor. Normally the resistor is connected at opposite ends. In this case it’s not, and I’m not sure why the resistance would be the same as if it were. Does the current still flow through the entire resistor?

 

[TSny]

The current first leaves the battery as shown below

Note that all of this current enters the core. Where does the current leave the core?

Think of the core as having a resistance which you found in part (a). So, you can think of the core as a resistor R_c. Likewise, the shell has an overall resistance R_a.

After the current leaves the core, where does it go?

 

[Schfra]

The current first leaves the battery as shown below
View attachment 224322

Note that all of this current enters the core. Where does the current leave the core?

Think of the core as having a resistance which you found in part (a). So, you can think of the core as a resistor R_c. Likewise, the shell has an overall resistance R_a.

After the current leaves the core, where does it go?

It would go through the shell. I’m guessing this means that the two resistors are in series?

I don’t quite understand why that’s the case. Since the wires aren’t attached at opposite ends wouldn’t the current not have to travel through the entire length of the resistors? And wouldn’t that make the resistance less than it would be in a situation where the current does have to flow through the entire length of the resistors?

 

[TSny]

The current enters the top of the core and leaves the core at the bottom. So, the current travels the entire length of the core. Then the current travels along the "short circuit" wire (which has negligible resistance) and enters the shell. Where does the current enter the shell? Where does it leave the shell? Does the current travel the entire length of the shell?

 

[Schfra]

The current enters the top of the core and leaves the core at the bottom. So, the current travels the entire length of the core. Then the current travels along the "short circuit" wire (which has negligible resistance) and enters the shell. Where does the current enter the shell? Where does it leave the shell? Does the current travel the entire length of the shell?

I believe the current enters the shell from the short circuit and then leaves into the negative terminal of the battery. So it does travel the entire length of the resistor.

Why though would it do that instead of just taking a straight path from the top of the two resistors? It seems like the electrons are not taking the path of least resistance.

 

[TSny]

The core and the shell are isolated from one another except for the short-circuit wire at the bottom. There is no "straight path from the top of the two resistors".

Often there is some sort of insulating material separating the core from the shell. Or, you can just think of there being an air gap between the core and the shell. Either way, current cannot travel between the core and the shell except through the wire at the bottom or through the wire and battery at the top. So, it's equivalent to

 

[TSny]

Here's a link to a nice diagram of a coaxial cable. The "metallic shield" is the shell.
https://en.wikipedia.org/wiki/Coaxial_cable#/media/File:Coaxial_cable_cutaway.svg