Levilaon said:
Ok with my calculations it comes again that time is infinite until velocity reach 0, what did you get?
I solved it like this: v=f(t), v₁=50, v₂=10, m=10, Fr=f(t)²
f(t)=v₁-a·∆t => f(t)=v₁- (f(t)²/m)·∆t => (∆t/m)⋅f(t)²+f(t)-v₁ = 0
So when velocity is f(t)=v₂ then: ∆t=(-10⋅f(t)+500)/f(t)² = 4s
And for distance: s=∫{0 to 4}(-1+√(1+4⋅(∆t/m)⋅v₁)/(2⋅∆t/m) d∆t ≈ 62.76
Your solution makes no sense and is incorrect. Do you know what is meant by a differential equation? Do you know how to solve the differential equation for v(t) in this problem? That was given in post #2.
If you do not know how to solve a differential equation, you can develop a finite-difference scheme to solve the problem approximately. For small ##\Delta t > 0## we have ##v(t+\Delta t) \doteq v(t) - \Delta t \cdot v(t)^2## (which becomes more and more nearly exact as ##\Delta t## gets smaller and smaller), so
$$ \begin{array}{rcl}
v(\Delta t) & \doteq &50 - \Delta t \cdot 50^2 \\
v(2 \Delta t)&\doteq& v(\Delta t) - \Delta t \cdot v(\Delta t)^2 \\
v(3 \Delta t) &\doteq& v(2 \Delta t) - \Delta t \cdot v(2 \Delta t)^2 \\
\vdots &\vdots & \vdots \\
v(N \Delta t) &\doteq & v((N-1) \Delta t) - \Delta t \cdot v((N-1) \Delta t)^2
\end{array}
$$
Be warned, however, that we need to take ##\Delta t ## very small to get any kind of decent accuracy. For example, we can take ##\Delta t = 1/1000 = 0.001## and ##N = 1000##, to get a good numerical solution over the interval ##0 \leq t \leq 1##, that is, at values ##t = 0, 0.001, 0.002, \ldots, 0.999, 1.000.## You could do all this in a spreadsheet.
There is also a simple exact formula for the solution ##v(t)##, but I think PF rules forbid me from telling you what it is.
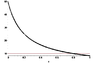
Below is a plot of the 1000-point curve of ##v(t)##, and the constant function v=10; you can see that ##v(t)## reaches 10 at about ##t = 0.8## sec. That is exact when we use the true formula for the exact solution.
BTW: the solution never reaches 0 exactly, just as you claimed.