- #1
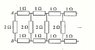
Resistor Network: Find the Equivalent Resistance Across AB
Click For Summary
Homework Help Overview
The problem involves determining the equivalent resistance across points A and B in an infinite resistor network. Participants are exploring various interpretations of the circuit and the implications of its infinite nature on resistance calculations.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation, Assumption checking
Approaches and Questions Raised
- Participants discuss initial confusion about where to start and question the relevance of certain resistors in the network. Some attempt calculations for finite segments of the network, while others suggest a recursive approach to define the total resistance. There is also mention of trends in resistance values as more resistors are added.
Discussion Status
The discussion is active, with participants sharing different perspectives and calculations. Some guidance has been offered regarding the recursive nature of the problem, but there is no consensus on the correct approach or final answer. Multiple interpretations of the resistance values are being explored.
Contextual Notes
Participants are grappling with the implications of an infinite resistor network and the assumptions that come with it. There is mention of a specific answer being suggested, but confusion remains about how to arrive at that conclusion.
