Bipolarity
- 773
- 2
If you have resistors in series ---\/\/\/\/---\/\/\/\/\/--- then the equivalent resistance of this system will merely be the sum of the individual resistors in the series. But the proof of this result is based on the fundamental assumption that the currents going through the two resistors (as well as through the equivalent resistor) are identical.
In the derivations for the equations of the Y-Δ transform, as shown in the picture
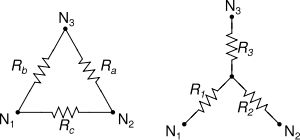 , the idea is that ## R_{c} = R_{1} + R_{2} ##. This follows from the fact that R1 and R2 are in "series", but they technically aren't since there is a branch coming out between them going to R3. They can only be in series if the current going through them is identical (this is the definition of series), but this implies that the current going through R3 is 0, which may not always be true!
, the idea is that ## R_{c} = R_{1} + R_{2} ##. This follows from the fact that R1 and R2 are in "series", but they technically aren't since there is a branch coming out between them going to R3. They can only be in series if the current going through them is identical (this is the definition of series), but this implies that the current going through R3 is 0, which may not always be true!
So what's the deal with this? It's been bothering me for a while as virtually no one has been able to explain this. Some people have said that for the sake of circuit analysis, the branch where R3 is located is totally ignored for the sake of evaluating ##R_{c}##, but I see no justification for this.
So either something is wrong with my understanding of the Y-Δ transform or something is wrong with my understanding of how series/parallel resistors really work. Which is it and why?
BiP
In the derivations for the equations of the Y-Δ transform, as shown in the picture
So what's the deal with this? It's been bothering me for a while as virtually no one has been able to explain this. Some people have said that for the sake of circuit analysis, the branch where R3 is located is totally ignored for the sake of evaluating ##R_{c}##, but I see no justification for this.
So either something is wrong with my understanding of the Y-Δ transform or something is wrong with my understanding of how series/parallel resistors really work. Which is it and why?
BiP