- #1
NewtonIsaac
- 5
- 0
Homework Statement
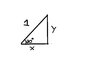
Find the components of the vector A with length a = 1.00 and angle=20.0° with respect to the x-axis as shown.
Enter the x component followed by the y component, separated by a comma.
Homework Equations
none
The Attempt at a Solution
To find the X-component I did the following:
cos20°=x/1
x=cos20°
x=.408082062
The Y-component was found in a similar fashion:
sin20°=y/1
y=sin20°
y=.912945251
My answer was entered as x,y substituting the relevant values in for x and y. However, the online system I'm using keeps telling me I'm wrong. Can anyone point me in the right direction?