Resolving Vector - Get Magnitude of F2 to 3 Sig Figs

[Lancelot59]

This should be a really simple problem, all I need to do is get magnitude of F2 along the axes u and v to 3 sig figs.

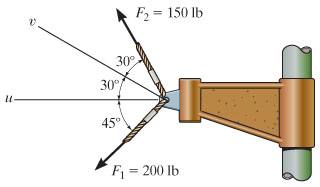
So I did the usual thing:

u=150cos(60)=75.0
v=150cos(30)=130

Is this wrong?

 

[Leveret]

It looks right to me. You may want to check your sig-figs, though.

 

[suwarna07]

yes its good

 

[Lancelot59]

Okay. I need to enter this stuff into an automated system called MasteringEngineering. It has a massive track record of being stupid with inputs. This just seemed a little too simple for it to mess up though. Thanks.

 

[rwisz]

Based on the given information, your calculation for the magnitude of F2 along the axes u and v appears to be correct. However, without more context or information about the vector F2, it is difficult to determine if this is the correct approach for resolving the vector. In general, resolving a vector involves breaking it down into its components along different axes or directions. The magnitude of F2 along the axes u and v can be calculated using the Pythagorean theorem as sqrt(u^2 + v^2). To ensure 3 significant figures, you may need to round your final answer to the appropriate decimal place. It is also important to carefully consider the units and any possible sources of error in your calculation. In any case, it is always a good idea to double-check your work and make sure you are using the correct equations and units.