Resonance in a Mechanical System

AI Thread Summary
The discussion revolves around calculating the length of a spring in a mechanical system where a mass is attached to it and revolves in a circle. The key equations involve the centripetal force and the spring force, leading to the equation -k*l = ω²*l*m. Participants highlight confusion regarding the use of the variable "l" and the unstretched length "l0." Clarifications suggest that the elastic force should be evaluated at the unstretched length, indicating that the spring's force does not depend on the total length. The conversation emphasizes the need to correctly define variables and forces to solve the problem effectively.
amk1995
Messages
4
Reaction score
0

Homework Statement


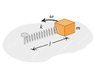
A mass m is attached to one end of a massless spring with a force constant k and an unstretched length l0. The other end of the spring is free to turn about a nail driven into a frictionless, horizontal surface. The mass is made to revolve in a circle with an angular frequency of revolution ω.
Question:
Calculate the length l of the spring as a function of ω.

Homework Equations


F = ω2*l*m
FSpring = k*l


The Attempt at a Solution


Fspring = Fcirc
-k*l = ω2*l*m

The issue I am having is how to get L by itself, or what I am supposed to do with l0. Can someone guide me on where I should head in order to solve this problem? The issue is l cancels when I divide, unless I am supposed to use l0 in place of l
Thanks!
 

Attachments

  • YF-13-44.jpg
    YF-13-44.jpg
    5.1 KB · Views: 612
Physics news on Phys.org
You are using "l" to designate two different things.
If "l" in the first equation is the total length of the spring (radius of the circle), then the elastic force is not correct. The force does not depend on the total length.
What is the force when the length is lo?
 
The force when length lo is just omega^2 *m*lo correct?
 
No. What is the elastic force ("produced" by the spring) when the spring's length is lo?
Hint: at lo the spring is unstretched.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Figure 1 Overall Structure Diagram Figure 2: Top view of the piston when it is cylindrical A circular opening is created at a height of 5 meters above the water surface. Inside this opening is a sleeve-type piston with a cross-sectional area of 1 square meter. The piston is pulled to the right at a constant speed. The pulling force is（Figure 2）： F = ρshg = 1000 × 1 × 5 × 10 = 50,000 N. Figure 3: Modifying the structure to incorporate a fixed internal piston When I modify the piston...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

How Does a Force Affect Spring Length Between Two Equal Mass Blocks?
Replies
2
Views
2K
Dynamics of a Block on top of a slab with friction between them
Replies
33
Views
1K
Potential energy in stretched spring
Replies
2
Views
2K
Rope on Table Kleppner-Mechanics
Replies
11
Views
3K
Initial Compressed Spring Force
Replies
3
Views
6K
Question about springs and rotational/translational energy
Replies
4
Views
1K
Stretching of a rotating spring
Replies
8
Views
2K
How Do Coupled Adiabatic Pendula Behave?
Replies
1
Views
1K
What Is the Frequency of Small Oscillations for a Pivoted Rod with Two Springs?
Replies
19
Views
2K
Dynamic system of self balancing robot
Replies
4
Views
731

Hot Threads

Recent Insights

Back
Top