HJKL
- 13
- 1
Homework Statement
:[/B]
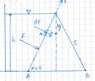
The cross-sectional profile of a dam is shaped as an isosceles triangle. The dam is standing on horizontal ground and the watermirror is as high as the top of the dam. The dam has height h, length l and the distance from the bottom to the watermirror along the dam's side is s. The water's density is ρ.
a) Find the resultant force from the water on the dam.
b) Find the resultant force's point of attack.
Homework Equations
[/B]
Don't know any relevant equations.
The Attempt at a Solution
[/B]
I do have the solution for this, but I don't understand the equations used and where they come from.
Solution:
a)
dA = l dx
dF = ρgy dA
dF = ρgy l dx
Similar triangles:
y/h = (s-x)/s <=> y = (h/s) (s-x)
dF = ρgl (h/s) (s-x) dx
Resultant force:
F = integral of dF from 0 to s
F = integral of ρgl (h/s) (s-x) dx
Then that is solved and we get (1/2)ρghls.
Where does that first equation come from? dA = l dx?
b)
The torque about an axis through the point A:
xF F = integral of x dF from 0 to s = integral of x ρgl (h/s) (s-x) dx
ρgl (h/s) ((1/2) sx^2-(1/3)x^3) from 0 to s
ρgl (h/s) ((1/2 s^3 - (1/3) s^3) = (1/6) ρghls
=> xF =((1/6) ρghls^2)/ ρghls => 1/3 s
The photo attached is the sketch of the dam.
Attachments
Last edited: