Resultant force projected along a line

[U1021981]

Homework Statement

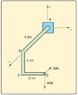
(i) Find the resultant force acting at point D and write it in Cartesian form. (Note that CD is parallel to the y-axis, the 40N force acts parallel to the z-axis and the 30N force is parallel to the x-axis.)

(ii) Find the magnitude of the projected component of the resultant force acting along the line AD.

Image of problem is attached.

Homework Equations

(i) Unsure about calculating resultant force
(ii) Find Unit vector of UAD and find the dot product of UAD and FR from (i)

The Attempt at a Solution

(i) Unsure if resultant force at point D is simply F1= (-30i) and F2= (-40k) so FR= (-30i - 40k) (Magnitude 50N) ?

(ii) UAD = (-0.2/0.245)i + (-0.1/0.245)j + (0.1/0.245)k

Then F.UAD = (Fi)(-0.2/0.245) + (Fj)(-0.1/0.245) + (Fk)(0.1/0.245)

Thanks for your help,

Tim

 

[gabbagabbahey]

(i) Unsure if resultant force at point D is simply F1= (-30i) and F2= (-40k) so FR= (-30i - 40k) (Magnitude 50N) ?

(ii) UAD = (-0.2/0.245)i + (-0.1/0.245)j + (0.1/0.245)k

Then F.UAD = (Fi)(-0.2/0.245) + (Fj)(-0.1/0.245) + (Fk)(0.1/0.245)

You have a sign error in your unit vector UAD, and I would recommend you include the units (Newtons in this case) in your expression for force and use exact numbers in your calculations. I get \frac{1}{\sqrt{6}}(2\mathbf{i}+\mathbf{j}-\mathbf{k}) for UAD.

 

[U1021981]

You have a sign error in your unit vector UAD, and I would recommend you include the units (Newtons in this case) in your expression for force and use exact numbers in your calculations. I get (1/√6)(2i+j−k) for UAD.

How did you calculate this?

I have used u = F(Coord)/F(magnitude) = (Fx/F)i + (Fy/F)j + (Fz/F)k

F (aka RDA) = (XA-XD)+(YA-YD)+(ZA-ZD)
= (0-0.2)+(0-0.1)+(0-(-0.1))
= -0.2i - 0.1j + 0.1k
magnitude = √0.06

Which is how I have got:

UDA = (-0.2/0.245)i + (-0.1/0.245)j + (0.1/0.245)k


Could you please outline the approach/steps that you believe I should take to solve the problem so I can get a better understanding.

Thanks for your reply,

Tim

 

[Luminous619]

How did you calculate this?

I have used u = F(Coord)/F(magnitude) = (Fx/F)i + (Fy/F)j + (Fz/F)k

F (aka RDA) = (XA-XD)+(YA-YD)+(ZA-ZD)
= (0-0.2)+(0-0.1)+(0-(-0.1))
= -0.2i - 0.1j + 0.1k
magnitude = √0.06

Which is how I have got:

UDA = (-0.2/0.245)i + (-0.1/0.245)j + (0.1/0.245)kCould you please outline the approach/steps that you believe I should take to solve the problem so I can get a better understanding.

Thanks for your reply,

Tim

Just on top of that, you have the same answers 2/√6 = .2/√.06

except in the drawing it shows that the pipe is +ve 0.2m (where you have -0.2m) and that if the line is in fact A to D then does it not share this property?

 

[gabbagabbahey]

How did you calculate this?

I have used u = F(Coord)/F(magnitude) = (Fx/F)i + (Fy/F)j + (Fz/F)k

F (aka RDA) = (XA-XD)+(YA-YD)+(ZA-ZD)
= (0-0.2)+(0-0.1)+(0-(-0.1))
= -0.2i - 0.1j + 0.1k
magnitude = √0.06

Notice first that \sqrt{0.06} = \frac{1}{10}\sqrt{6}. Next, consider that UAD usually means "the unit vector from A to D". By using RDA as F, instead of RAD, you've calulated the opposite and hence have a sign error.