- #1
Jgolf
- 11
- 0
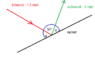
please help as I'm very old but play Pickleball which is similar to tennis but with a plastic whiffle ball and a solid racket on a reduced size modified tennis court. What I'm trying to figure out is the following: a player on the other side of the net and to the left of me returns the ball that is 135 degrees to where I want to return his shot. The ball is traveling back to me at 1.5 mph. My solid racket will contact the ball returning the ball with a force of 3 mph and facing the the same 135 degrees. Therefore attempting to the ball straight ahead...However, what angle will the ball leave the racket? I know that the return shot will not be 90 degrees of where the racket is facing...trying to figure out what the angle the ball leaving the racket will have...many thanks for anyone who can help me...John