Snell's law problem about the angle of a wave and the coast

[Nightsheron]

Homework Statement

First question:
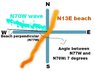
The waves are approaching at an bearing of N70W, and at N50W, to a coast with a N13ºE orientation. What is the angle of the wave offshore?
Answer: 7 degrees and 27 degrees.

Second question:
The wave is approaching at an angle of 135º. The coast is at 305º. What is the angle of the wave offshore?
Answer: 80 degrees.

Third question (now the total confusion):
The beach is facing north-south. The wave is approaching at an angle of 277º, and 230º. What is the angle of the wave offshore?
Answers: 7º and 40º.

Fourth question:
The wave is breaking in a coast with a East-West orientation, having a N10E bearing. What is the breaking angle?
Answer: 10º.

Fifth question:
What is the incidence angle on open waters of a wave with a bearing of 130º, in a coast with a direction of 80º?

Homework Equations

This is the formula we used at class:
Velocity of the wave offshore (as it is coming from the ocean) / Velocity of the wave when it is breaking = Sine of the angle of the wave offshore (as it is coming from the ocean) / Sine of the angle of the wave when it is breaking

The Attempt at a Solution

First question:
Here's how I THINK the answer could have been achieved. I am just to convert the N70W to azimuth; it becomes 290, then I subtract 90 degrees until I get to a angle that is within 90º of the other one. Then I can subtract, that is, 20-13=7. But I do not know if this is the right method.

Second question:
My thinking: 305-90= 215 ; 215-135=80

Third question:
I don't know. If I use the above method, it works for the first angle, but the second angle would give me 50 degrees instead.

Fourth question:
This one seems straightforward but I am not going to assume anything!

Fifth question:
I don't know neither the answer nor how it is supposed to be done.

My teacher talked something about a projection, is it a orthogonal projection or...? He also talked something about drawing a perpendicular to a coast?
I can't find anything on the web that is similar so I can figure it out. PLEASE help. If someone could give me the name of this kind of exercise, and some explained examples, I could try, but I haven't found much after hours of searching.

I have tried solving this, but I don't know if I am right or not.

I've been pulling my hairs for these ones! I have spent many a good hours on this, almost the entire day actually. If it didn't come through as I wrote the post, note the time here in Portugal is 4:30 AM. :(

Sorry if the wording seems odd, as I have translated it from Portuguese.

Thanks very much.

 

[Dr. Courtney]

Seems like some careful diagrams would help.

 

[Nightsheron]

I made a diagram for one of the cases, I'll make some more, but am I on the right track so far? I haven't got much of a clue to be honest with you.

SEE DIAGRAM IN ATTACHMENT.

Seeing it a little different now than I was at the OP, I first drew the beach at the orientation given. (I drew it through the other quadrant as well, since the beach is not in just one quadrant right?). Then I drew the wave. Then I drew a perpendicular of the beach: this is what I don't know the reasoning behind, but I remember we did something like this in class. Explanation please? Then I just measured from one angle to the other one.

Tried to make it somewhat clean for educational purposes, maybe someone else will have this question one day. :D