michaelw
- 80
- 0
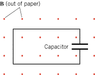
Indicate the direction of the electric field between the plates of the parallel plate capacitor shown in the drawing if the magnetic field is decreasing in time. Give your reasoning
if the magnetic field is decreasing, so is the flux, so mr. lenz says the induced magnetic field must be out of the page to counteract the decreasing flux
but with right hand rule #2, it completely depends where you put your hand in determining the direction of current
if you put it at the top of the the wire, curl fingers out of page, current goes to the right (right hand, conventional current).. ie) clockwise
if you put it at the bottom, current still goes to the right, but now it means the direction is counter clockwise.
which is right and why??

if the magnetic field is decreasing, so is the flux, so mr. lenz says the induced magnetic field must be out of the page to counteract the decreasing flux
but with right hand rule #2, it completely depends where you put your hand in determining the direction of current
if you put it at the top of the the wire, curl fingers out of page, current goes to the right (right hand, conventional current).. ie) clockwise
if you put it at the bottom, current still goes to the right, but now it means the direction is counter clockwise.
which is right and why??