How Should You Approach Fitting Multiple Gaussians to Data with Poisson Errors?

[Malamala]

Hello! I have the to fit a curve to the attached data (I plotted it both with and without error bars), where the error bars are Poisson errors i.e. $\sqrt{N}$, where $N$ is the number of counts in the given bin. I want to fit 3 Gaussians + background and extract the values (and errors associated) of the 3 means and 3 standard deviations. This is the raw data that I was provided with i.e. I was given the number of counts for each value of the x-axis (I don't have the individual values for each element in each bin). What is the best way to fit it? There are many bins with very low count, so I can't assume that the Poisson error is a Gaussian there (<10 data points) so doing a least-square fit might be a bit tedious. Also I am not sure how well it would perform, given that the relative errors are quite big so the relative errors on the parameters of the fit will also be large. I was thinking to re-bin the data. I would reduce the relative error in each bin, but I am not sure what is the right way to do it. Different binnings give slightly different values for the means and standard deviations and I am not sure which one should I pick or how to combine the values from different binnings to give a final value. I guess I can't use max-likelihood here, given that I don't have the individual measurements. What should I do? Thank you!

 

[BvU]

Nice data ! The plot thickens as they say in detective novels !

I was given the number of counts for each value of the x-axis (I don't have the individual values for each element in each bin)

Not clear to me what you do have available.

Basically you have to minimize your $\sum (y_\text{predicted} - y_\text{measured})^2/y_\text{measured}$ with $y_\text{predicted}$ calculated from a ten-parameter model (three Gaussians and a flat background). That is, if you have all raw data available. Re-binning would not improve the accuracy of the fit results.

I seem to remember Bevington: Data Reduction And Error Analysis ... (I have a copy from the 1969 1^st edition ) works out an example of a peak on a quadratic background.

 

[Malamala]

Nice data ! The plot thickens as they say in detective novels !
Not clear to me what you do have available.

Basically you have to minimize your $\sum (y_\text{predicted} - y_\text{measured})^2/y_\text{measured}$ with $y_\text{predicted}$ calculated from a ten-parameter model (three Gaussians and a flat background). That is, if you have all raw data available. Re-binning would not improve the accuracy of the fit results.

I seem to remember Bevington: Data Reduction And Error Analysis ... (I have a copy from the 1969 1^st edition ) works out an example of a peak on a quadratic background.

So the raw data that I have, is the data that I plotted. What I meant is that for a bin with 60 counts in the plot I attached, I don't have the individual 60 entires, I just have the pair, say, (9000, 60).

You are right, rebinning doesn't add new information (actually makes you lose some), my issue is with the error bars (which actually appear, too, in the formula that you mentioned). In Bevington the background has 1 or 2 points with few counts, so assuming Gaussian errors would be ok overall. My plot has lots of points with less than 10 counts. If I do the fit the way it is now, I get a pretty big relative error on the parameters (due to error propagation). If I re-bin, the error goes down, but the value of the parameters themselves changes slightly, too (basically rebinning shits the center of the peak and modify its width). So I am not sure what to do? Should I fit it like this? Should I rebin the data until I have at least 10 counts per bin? Should I do something else?

 

[BvU]

If I do the fit the way it is now, I get a pretty big relative error on the parameters (due to error propagation)

Didn't expect that (-- perhaps it's because these errors on the parameters are correlated ? )

But re-binning doesn't have to be done for all the bins; if you only do it for bins with < 10 entries the peak widths and positions should come out of the fit unaffected. And the peak areas are large enough too.

@mfb : to me this looks like a good dataset for fitting; any suggestions ?

 

[BWV]

If this is some sort of arrival rate-type data, there is an explicit poisson regression:

https://en.wikipedia.org/wiki/Poisson_regression
the glm functions in R and Matlab have options for this

 

[Malamala]

If this is some sort of arrival rate-type data, there is an explicit poisson regression:

https://en.wikipedia.org/wiki/Poisson_regression
the glm functions in R and Matlab have options for this

I am not sure what is arrival rate-type data. This is just counts data. For example scanning some energy range and counting the number of certain events.

 

[BWV]

I am not sure what is arrival rate-type data. This is just counts data. For example scanning some energy range and counting the number of certain events.

A standard application / example for Poisson dist is the number of arrivals per interval of time, like cars at a toll booth. Your data seems similar - all positive integer values

 

[gleem]

Have you actually tried to fit the data? You have so many data points (degrees of freedom) that the error in each point should not have a large effect on the uncertainty of the fitted parameters. I do not know why you are concerned with the background. It is so low relative to the signal that it should have a minimal effect on the peak parameters.

 

[gleem]

What information is of most important concern? You mentioned counting data. Is this of a nuclear reaction origin? If so the total number of counts under the peaks would be of interest but there are so many that the statistical error should be low relative to other errors as the efficiency of the system or other peak count corrections. Peak position might be of interest but again other errors as linearity of your equipment might be larger than the estimated uncertainty of the fit. As far as the data is concerned I would fit it and not worry too much about the effects your error assumptions. Looking at the residuals of the fit (data -fit)/σ for significant deviations to identify areas that have not be fitted well regionally.

 

[Stephen Tashi]

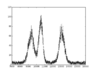
Hello! I have the to fit a curve to the attached data (I plotted it both with and without error bars), where the error bars are Poisson errors i.e. $\sqrt{N}$, where $N$ is the number of counts in the given bin. I want to fit 3 Gaussians + background and extract the values (and errors associated) of the 3 means and 3 standard deviations.

Usually if someone says they want to fit 3 probability distributions to a set of data, they mean that the data represents the realizations of a single (scalar) random variable. In such a situation, this is a question of modeling one probability distribution as a "mixture" of other probability distributions. There is lots of literature on how to fit mixture distributions to such data.

An example of this type of problem would be:
There are 3 factories, A,B,C that each make widgets.
The weight of a widget made by each factory is a normally distributed random variable.
The normal distributions for the factories may be different.
We have a data consisting of a histogram of widget weights for a months production of the 3 factories. The data gives the weights of 1000 widgets.
The data doesn't not specify which factory made each widget. So, for example, if the data says 40 widgets have a weight between 90.2 and 90.3 kilograms, we don't know how many of these widgets were made in factory A.

Our task is create a probability model that estimates parameters for three normal distributions and the fraction of the 1000 widgets that were chosen from each of these distributions. (We won't be able to say which normal distribution applies to factory A. We only attempt to identify 3 different normal distributions, not to assign each of the distributions to a specific factory.)

The scalar random variable can be defined as "Pick a widget at random from the 1000 widgets and measure its weight".

However, you haven't clearly described your data. Perhaps it does not represent realizations of a single scalar random variable. If it doesn't, you need to explain the data.

Suppose we do an experiment where two marbles collide and smash into a finite number of pieces. On each experiment we record the kinetic energy of each piece. We do 1000 experiments. We combine all this data into a histogram where the x-axis represents kinetic energy and the y-axis represent how many times we observed a piece to have this kinetic energy.

The above situation is not a histogram of realizations of a single scalar random variable. Each experiment can be regarded as producing a random vector of results.

In the case of a histogram of data for a single scalar random variable, if we see it's shape looks like 3 gaussian distributions averaged together, it's reasonable to fit a "mixture" model to the data. However, if the histogram comes from random vectors of data, it isn't so simple to justify fitting a mixture model.

 

[Malamala]

@BvU @gleem Thank you for replies (and sorry for replying so late). So I created some mock data on my own similar to the one I showed in my original post and I fitted the data with 3 Gaussians + background for the same binning as in the original post, half the number of bins (so double bin size) and 1/3 the number of bins (triple bin size). These are the parameters of the simulated data:
mu_1 = 9356
sigma_1 = 340
mu_2 = 10520
sigma_2 = 240
mu_3 = 13103
sigma_3 = 320

and these are the results of the 3 fits (done with the lmfit python package):

Original bin size data:
mu_1 = 9343.368024925216 +/- 23.7795988643757
sigma_1 = 373.37180944261706 +/- 25.054822826597437
mu_2 = 10520.008834943186 +/- 16.296494879212197
sigma_2 = 248.95355107786207 +/- 15.038076584932401
mu_3 = 13079.617291492405 +/- 20.678223331317835
sigma_3 = 342.87157208169833 +/- 19.81801921769196

Double bin size data:
mu_1 = 9347.541487314367 +/- 22.554543873976304
sigma_1 = 364.2159608392336 +/- 23.639726774889134
mu_2 = 10518.672637588254 +/- 16.031782443319145
sigma_2 = 250.11736485722992 +/- 14.91507790224974
mu_3 = 13084.159070450844 +/- 19.897825608583876
sigma_3 = 337.16829832214177 +/- 19.02302371330743

Triple bin size data:
mu_1 = 9344.847309694578 +/- 21.887456335048064
sigma_1 = 358.45903288769614 +/- 22.791553461866997
mu_2 = 10519.310656847158 +/- 15.735789892687324
sigma_2 = 246.67432694916502 +/- 14.611855849087197
mu_3 = 13086.736664298349 +/- 20.198699556016283
sigma_3 = 338.2233185803001 +/- 19.297874643744954

If I were to say, the first one looks the worst (look at the value of sigma_1 for example). So this is why I was tempted to re-bin my data, as the results seem to be better in that case. What do you think? Would you use the number from the original binning? I also attached the fits. Thank you!

 

[BvU]

the first one looks the worst

We have a different attitude with respect to statistics. If I look at the results I see

9343    373    10520    249    13080    343
9348    364    10519    250    13084    337
9345    358    10519    247    13087    338

And all three fits give exactly the same result.

What worries me enormously is that you

1. present these outcomes in 16 digits (would you present them in 64 digits if they were output in 64 ?)
2. See differences that are the size of 1/3 $\sigma$ and are tempted to consider them different

   So this is why I was tempted to re-bin my data, as the results seem to be better in that case

3. Only show 6 of the fitted parameters (you did fit 10 parameters, I hope ?) ( also a bit because it prevents me from plotting the three peaks and thus visualizing my 'exactly the same' claim)
   

 

[Malamala]

We have a different attitude with respect to statistics. If I look at the results I see

9343    373    10520    249    13080    343
9348    364    10519    250    13084    337
9345    358    10519    247    13087    338

And all three fits give exactly the same result.

What worries me enormously is that you

1. present these outcomes in 16 digits (would you present them in 64 digits if they were output in 64 ?)
2. See differences that are the size of 1/3 $\sigma$ and are tempted to consider them different
3. Only show 6 of the fitted parameters (you did fit 10 parameters, I hope ?) ( also a bit because it prevents me from plotting the three peaks and thus visualizing my 'exactly the same' claim)

Thank you for your reply! Sorry for the digits, I just picked the python output, without thinking to truncate it. I also attached the data if it is useful (and yes I fitted all parameters; there are actually 11 as for the background I decided to use a+bx, not just a constant). The reason why I said that the first fit is not great is that, for example, sigma_1 = 373 +/- 25 while the true value is 340. I know that one sigma and a half is not a lot, it's just that it is worse than the rest (which are less than one sigma away from the true value). Also the error on the parameters is smaller for less bins. I guess that my question is, if in this case I know that I don't have any finer structure that could be lost by rebinning, and that the fit seems to be (slightly) more confident about the parameters when I rebin, while still giving the right result within the error, why would I not rebin? (I am sorry for asking so many questions, I am really new to data analysis in general and I want to understand how and why to do certain things). Thank you!

 

[BvU]

which are less than one sigma away from the true value

One sigma means 68% is within $\pm 1\sigma$ -- so you don't worry about one case that deviates a bit more.

actually 11 as for the background I decided to use a+bx

Why ? And how do you reason that 11 parameters is better than 10 ?

the error on the parameters is smaller for less bins

I don't see that. How big do you think the error on the error is ? Double-size bins make it a little easier for the fit, which works out minimally favourable for the first peak but does nothing for the other two. My conclusion: statistical noise.

Also, you reduce the number of degrees of freedom by double-size or triple-size binning, so the reduced chi squared for the fit should come out higher.

There is no argument for double binning at all: all bins have more than 32 counts, so assumption Poisson = Gauss is OK

And -- if you are forced to do double-binning, you do so only for bins where there are less than 10 counts, not for the other bins.

 

[gleem]

I know that one sigma and a half is not a lot, it's just that it is worse than the rest

But is that significant? You are biased since you know the true value. Repeat the simulation without binning and see what you get. One observation, peak one is fairly close to peak two and their parameters are probably more correlated. What is the manner of the way the fit is made with the Python Imfit with which I am not familiar

 

[Malamala]

One sigma means 68% is within $\pm 1\sigma$ -- so you don't worry about one case that deviates a bit more.
Why ? And how do you reason that 11 parameters is better than 10 ?
I don't see that. How big do you think the error on the error is ? Double-size bins make it a little easier for the fit, which works out minimally favourable for the first peak but does nothing for the other two. My conclusion: statistical noise.

Also, you reduce the number of degrees of freedom by double-size or triple-size binning, so the reduced chi squared for the fit should come out higher.

There is no argument for double binning at all: all bins have more than 32 counts, so assumption Poisson = Gauss is OKView attachment 250764

And -- if you are forced to do double-binning, you do so only for bins where there are less than 10 counts, not for the other bins.

Thanks a lot for this explanation! It really helped. One more thing, it might be the case (not here, but in the future), that the x-axis has an error, too (for example related to the resolution of the detector used to measure the energy). Could you please give me any suggestion on how to proceed in that case? Is it still ok to keep the same number of bins (if I group them the error on the x-axis would go down as $\sqrt{n_{bins}}$, where $n_{bins}$ is the number of bins I group together)? And how should I handle the error on the x axis? Can I assume that x has no error and transfer it to y (I think I read this in Bevington, but not sure), as $\sigma_y^{total} = \sqrt{\sigma_x^2 + \sigma_y^2}$?

 

[BvU]

Can I assume that x has no error and transfer it to y (I think I read this in Bevington, but not sure), as $\sigma_y^{total} = \sqrt{\sigma_x^2 + \sigma_y^2}$

This is not right: check the dimensions ! Since $y$ is a function of $x$, there should be at least something like $(f'(x)\sigma_x)^2$ there instead of just $\sigma_x^2$.

But it doesn't help much, since the scatter in $x$ will smear out the peaks anyway.
So you better stay away from bin sizes $<<$ resolution

 

[Malamala]

This is not right: check the dimensions ! Since $y$ is a function of $x$, there should be at least something like $(f'(x)\sigma_x)^2$ there instead of just $\sigma_x^2$.

But it doesn't help much, since the scatter in $x$ will smear out the peaks anyway.
So you better stay away from bin sizes $<<$ resolution

Oh ok, but don't I need to take the error in x into account when I do the least-square fit (or likelihood fit) regardless of the bin size? How do I do that?

 

[BvU]

How do I do that?

Don't understand the question. You didn't take error in x into account when you did your fits until now, didn't you ?

 

[Malamala]

Don't understand the question. You didn't take error in x into account when you did your fits until now, didn't you ?

Sorry, what I meant is, if you have error bars on both x and y variables for each data point, how do you take that into account when you do a least-square fit? In the data I asked about here, there is no error on the x, so I didn't worry about it, but I am asking in general (not only for histograms, necessarily, but for any data points with errors in both directions). I've also noticed that all the programs that I've ever used for fits accept as weights (which are usually used for the $1/\sigma^2$ term) only one list, which is for the error on y, so I don't even know how would I pass the error on x to such a built-in program.

 

[Stephen Tashi]

Don't understand the question.

You understand the original post well enough to have ideas about solutions. Can you explain what the data is? @Malamala hasn't said.

What is the manner of the way the fit is made with the Python Imfit with which I am not familiar

Parroting from https://www.mpe.mpg.de/~erwin/code/imfit/ :

Imfit is a program for fitting astronomical images -- especially images of galaxies, though it can in principle be used for fitting other sources. The user can specify a set of one or more 2D image functions (e.g., elliptical exponential, elliptical Sérsic, circular Gaussian) which are added together to generate a model image. This model image is then matched to the input image by adjusting the 2D function parameters via nonlinear minimization of the total χ2.

That would be clear if "image functions" were defined. The format of images is typically given by one or more "intensity" values for each pixel. The terminology "counts" is being used in this thread.

Suppose I have a deterministic model that gives a count or intensity for each pixel in set of pixels. The difference in the models predicted intensity at a pixel and the actual intensity measured in a image can be regarded as an "error". However, such a deterministic model provides no information about a probabilistic cause for this error. If the predicted intensity or count at a pixel is 100, there is no justification (in the model) for taking 100 to be the parameter $\lambda$ for a Poission distribution and concluding that the standard deviation of the "error" at that pixel is $\sqrt{\lambda}$.

If the observed intensity or pixel count at a pixel is 100 then one might assume that the data is generated in a stochastic manner and that 100 is a good estimate for the parameter $\lambda$ of a poisson random variable that generates the data for that pixel. However the standard deviation $\sqrt{\lambda}$ refers to the standard deviation of the observed data about the actual mean intensity at that pixel. It does not refer to the standard deviation of stochastically generated data about the predicted mean intensity given by the the model.

In different thread (https://www.physicsforums.com/threads/confused-about-systematic-errors.978151/ ) the OP asks about "systematic" errors and in yet another thread ( https://www.physicsforums.com/threads/poisson-error-question.978464/ ) the OP asks about stating an "uncertainty" for a predicted value. Perhaps the OP wants to state the predicted intensity of each pixel and give an estimate for the standard deviation for stochastically generated data about that predicted value ( as opposed to giving an estimated standard deviation for stochastically generated data about the actual mean value used by a stochastic procedure that generates the data.)

 

[Malamala]

You understand the original post well enough to have ideas about solutions. Can you explain what the data is? @Malamala hasn't said.
Parroting from https://www.mpe.mpg.de/~erwin/code/imfit/ :That would be clear if "image functions" were defined. The format of images is typically given by one or more "intensity" values for each pixel. The terminology "counts" is being used in this thread.

Suppose I have a deterministic model that gives a count or intensity for each pixel in set of pixels. The difference in the models predicted intensity at a pixel and the actual intensity measured in a image can be regarded as an "error". However, such a deterministic model provides no information about a probabilistic cause for this error. If the predicted intensity or count at a pixel is 100, there is no justification (in the model) for taking 100 to be the parameter $\lambda$ for a Poission distribution and concluding that the standard deviation of the "error" at that pixel is $\sqrt{\lambda}$.

If the observed intensity or pixel count at a pixel is 100 then one might assume that the data is generated in a stochastic manner and that 100 is a good estimate for the parameter $\lambda$ of a poisson random variable that generates the data for that pixel. However the standard deviation $\sqrt{\lambda}$ refers to the standard deviation of the observed data about the actual mean intensity at that pixel. It does not refer to the standard deviation of stochastically generated data about the predicted mean intensity given by the the model.

In different thread (https://www.physicsforums.com/threads/confused-about-systematic-errors.978151/ ) the OP asks about "systematic" errors and in yet another thread ( https://www.physicsforums.com/threads/poisson-error-question.978464/ ) the OP asks about stating an "uncertainty" for a predicted value. Perhaps the OP wants to state the predicted intensity of each pixel and give an estimate for the standard deviation for stochastically generated data about that predicted value ( as opposed to giving an estimated standard deviation for stochastically generated data about the actual mean value used by a stochastic procedure that generates the data.)

The origin of the data is not really relevant for my question, but you can think of it as a particle physics counting experiment, or something where you obtain clear peaks. The link that you provided is not the lmfit that I am using. As mentioned above, I am using the python fitting package lmfit: https://lmfit.github.io/lmfit-py/ But again, the package I am using for fitting (even the programming language) is irrelevant for my question. I mentioned it just for completeness.

 

[Stephen Tashi]

The origin of the data is not really relevant for my question, but you can think of it as a particle physics counting experiment, or something where you obtain clear peaks.

That is isn't a sufficient description. Is the data from a single experiment? - one experiment that measures "counts" at a given set of frequencies? Or is the data a summary of several different experiments?

What does the curve that is fit to the histogram represent? Is the value given by the curve a deterministic prediction of the number of counts? Or is the predicted value at a pixel supposed to be the mean count for some stochastic process that generated the data? Are you requiring that the curve produce only integer values?

Suppose the data is from one experiment and you are assuming the data for each frequency was generated by a poisson process ( with possibly different parameters for different frequencies) and the curve that is fit makes a deterministic prediction for the count at each frequency - and you desire to publish the predicted count plus the "uncertainty" associated with that count. This amounts to the same situation that I described in my previous post. Instead of pixels, you have "bins" of frequencies.

 

[Malamala]

That is isn't a sufficient description. Is the data from a single experiment? - one experiment that measures "counts" at a given set of frequencies? Or is the data a summary of several different experiments?

What does the curve that is fit to the histogram represent? Is the value given by the curve a deterministic prediction of the number of counts? Or is the predicted value at a pixel supposed to be the mean count for some stochastic process that generated the data? Are you requiring that the curve produce only integer values?

Suppose the data is from one experiment and you are assuming the data for each frequency was generated by a poisson process ( with possibly different parameters for different frequencies) and the curve that is fit makes a deterministic prediction for the count at each frequency - and you desire to publish the predicted count plus the "uncertainty" associated with that count. This amounts to the same situation that I described in my previous post. Instead of pixels, you have "bins" of frequencies.

Why would it matter if it's one or more experiments? You can assume there are more and the data is combined or it's just one and this is the whole data, I am not sure I see how would that change the fitting procedure. And the curve is just a fit to those points. What I need is the center of the 3 peaks. If there is a way to get that center (and the errors associated to it) without fitting a curve to the points, that's fine, too. But as far as I know fitting a curve and extracting the parameters is the way it is usually done. I am not sure I understand your questions about the role of the curve. The curve is just the best fit to the points. I don't even really see how can you require it to take only integer values. It wouldn't be smooth anymore, while the function that I need (3 Gaussians + background) is obviously smooth. Again my main question is, what is the best way to extract the mean values and the associated errors from the data I showed.

 

[Stephen Tashi]

Why would it matter if it's one or more experiments?

If you had more than one experiment producing a count for a given frequency $x_1$, you'd have data for a better estimate for the variance of the counts at $x_1$ - better than just having the results from a single experiment.

And the curve is just a fit to those points. What I need is the center of the 3 peaks. If there is a way to get that center (and the errors associated to it) without fitting a curve to the points, that's fine, too. But as far as I know fitting a curve and extracting the parameters is the way it is usually done.

As I've said previously, statistics is subjective. From the point of view of publishing something, it is important follow the traditions used in your field of study and in the particular journal you wish to publish in. So I agree that you should should do things the way other published papers in your field do them. You should also present anything involving "uncertainties" the way other published papers present it. If other papers don't explain how they arrived at their "uncertainties", it's reasonable to email the authors and ask how they did it.

Again my main question is, what is the best way to extract the mean values and the associated errors from the data I showed.

Asking for the best way to do something is a understandable as a human motivation. However , "best" is not a specific property in mathematics - especially in statistics. To ask for the "best" way, suggests that you want to optimize some function, but until that function is defined, "best" is an ambiguous criteria.

I writing "uncertainty" in quotes, because what you mean by that word is unclear. (Likewise "errors" isn't specific.) Since this section covers probability and statistics, a reader is tempted to interpret an "uncertainty" as a standard deviation of a random variable - or some estimate of that standard deviation However, you have not defined any random variable. You don't want to formulate the problem using a specific probability model. I don't blame you for that. Probability models can get complicated. However, if you want to define "the best way" to mean "the way that's most likely to be correct", you are introducing a statement about a probability of something happening. So you can't avoid talking about random variables.

It doesn't hurt to ask forum members for advice. But concise advice about how to do things won't include a mathematical demonstration that's it's the appropriate thing to do. If you follow the advice and someone questions your work, you won't have any ammunition for defending it.

 

[Malamala]

If you had more than one experiment producing a count for a given frequency $x_1$, you'd have data for a better estimate for the variance of the counts at $x_1$ - better than just having the results from a single experiment.
As I've said previously, statistics is subjective. From the point of view of publishing something, it is important follow the traditions used in your field of study and in the particular journal you wish to publish in. So I agree that you should should do things the way other published papers in your field do them. You should also present anything involving "uncertainties" the way other published papers present it. If other papers don't explain how they arrived at their "uncertainties", it's reasonable to email the authors and ask how they did it.
Asking for the best way to do something is a understandable as a human motivation. However , "best" is not a specific property in mathematics - especially in statistics. To ask for the "best" way, suggests that you want to optimize some function, but until that function is defined, "best" is an ambiguous criteria.

I writing "uncertainty" in quotes, because what you mean by that word is unclear. (Likewise "errors" isn't specific.) Since this section covers probability and statistics, a reader is tempted to interpret an "uncertainty" as a standard deviation of a random variable - or some estimate of that standard deviation However, you have not defined any random variable. You don't want to formulate the problem using a specific probability model. I don't blame you for that. Probability models can get complicated. However, if you want to define "the best way" to mean "the way that's most likely to be correct", you are introducing a statement about a probability of something happening. So you can't avoid talking about random variables.

It doesn't hurt to ask forum members for advice. But concise advice about how to do things won't include a mathematical demonstration that's it's the appropriate thing to do. If you follow the advice and someone questions your work, you won't have any ammunition for defending it.

I guess it would be better to put it this way: if someone gave you the data points I showed above, from a single experiment (say a counting experiment, and this is all the available data), and you'd want to publish a paper (say in a common, respectable journal Nature, Science, PRL etc.) in which to present the values of the peaks (e.g. mass of a resonance), how would you do it?

 

[Stephen Tashi]

I guess it would be better to put it this way: if someone gave you the data points I showed above, from a single experiment (say a counting experiment, and this is all the available data), and you'd want to publish a paper (say in a common, respectable journal Nature, Science, PRL etc.) in which to present the values of the peaks (e.g. mass of a resonance), how would you do it?

I'm not in academia, but imagining myself in that situation, I'd follow my own advice. I'd look at other published papers and see what they did. If the papers didn't explain their procedures, I'd politely ask some of the authors about how calculations were done.

Having an interest in probability and statistics, it's difficult to resist inventing a method myself - without regard to whether any journal would like it. One idea is to fit a curve (from the family of curves you have specified) that minimizes the $\chi^2$ statistic instead of achieving least square errors. That approach treats the curve fit as a probability model that gives the parameter $\lambda_i$ for a Poisson distribution of counts that (we imagine) is sampled to give the count for the $i$th frequency bin.

What I need is the center of the 3 peaks.

From the curve fit, we get a probability model for how the data is generated and the mean frequency of the 3 peaks. As to estimating the individual $\lambda_i$ and estimating their standard deviations, is it necessary (i.e. is it traditional) to publish such information? For now, I'll just worry about the estimate of center of the 3 peaks and estimating the standard deviation of that estimate.

In the case of estimating a standard deviation for parameters that fit a curve to data, all the methods I know involve a form of reasoning that sounds self contradictory when it is plainly stated. When we use a software that spits out an estimate for the variability of the parameters, we can quote the results without embarassing ourself by explaining how they were derived. The reasoning amounts to this: "Assume the parameters for the curve fit are roughly correct. Then I'll give you an estimate of how much they can be off."

You mentioned doing Monte Carlo studies, so the method should be familiar. Use the fitted curve to define parameters for Poisson distributions at each frequency. Generate sets of pseudo-data from these parameters. Fit a curve to each set of pseudo data and compute the "center" for each curve. Take the set of centers and find the standard deviation of the difference between those centers and the center for the curve fit to the real data. Assume this standard deviation is a good estimate for the standard deviation between the physically "true" center and the center given by a curve fit to real data.

There a commonsense argument in favor of this type of reasoning. If the real data is some sort of freak occurence, we aren't going to get reliable estimates from it. So we may as well assume it is approximately representative of an underlying probabilitiy model.

I'm not a nuclear physicist. If I were, I wouldn't let myself be lobotomized by statistical procedures. I'd consider whether the above model makes sense in physics. In particular there is the question of how a Poisson process with parameter $\lambda_i$ creates the count in a bin of frequencies. In typical applications $\lambda_i$ is a parameter related to counts per unit time or counts per unit area etc. If we apply the model to a bin of 10 consecutive frequencies we are regarding $\lambda_i$ as parameter related to "counts per unit frequency". Does this make physical sense?

 

[BvU]

So the raw data that I have, is the data that I plotted

Why change to mock data in #11 ? Or are #1 data mock data too ?

am not sure what is arrival rate-type data. This is just counts data. For example scanning some energy range and counting the number of certain events.

Your data is what BWV calls arrival rate-type: a count accumulated over a certain time interval. But I expect you know by now.

I strongly agree with @gleem #9 : fit and look at the outcome.

Anxious to see your 11 fitted parameter values (not just 6) and the corresponding chisquared.
And their input values for generating the mock data.
[edit]reason: to me it (#11) does not look like a good fit result

 

[gleem]

@Stephen Tashi a man after my own heart wrt fitting if I read you correctly.

I spent many many hours fitting data from a magnetic spectrograph; data much like yours @Malamala where the abscissa was energy of particles from a nuclear reaction and the ordinate counts per unit energy interval.
Perhaps if I recount my experiences in fitting my data it may be of value to you or others for that matter.

So let me list the concerns I had . I had to verify the line shape of peaks. There is a instrumental response function that is the line shape of a peak from a monoenergetic particle. I had to determine how this changed with varying experimental conditions and how these conditions modified the line shape and affected the parameters of interest. I had to gain confidence with the computer fitting programs estimate of parameters by fitting trusted data (I did simulations like you did but I needed to believe it predicted real world data). I had to make sure the deterministic distribution (modified Lorentzian) did not pose problems( strongly overlapping) and when it did to understand them and the affects on the parameters. I had to understand correlations among parameters and try to avoid correlations if possible.

I used a gradient search program to minimize Chi Square. I introduced constraints where possible to help the program run faster and prevent it from becoming "lost" i.e., stuck in a local Chi Sq. minimum. I often fit multiple spectra simultaneously for example with data in which certain parameters were the same. To find if there were areas of the spectrum than might not be well fit I looked at the residuals from the fit. In particular I calculated the Chi Sq of a running average along the spectra looking for unusual values for Chi Sq. Finding several contiguous outliers raised suspicion and instigated an investigation to resolve this.

Of course all data is different but one thing is clear you should understand all aspects of it. You should make sure your fitting program is doing what you think it should be doing. Experiment with it. Use as few parameters as possible. Some parts of spectra cannot be described by anything you know e.g. background over short distance might be constant or linear over large distances there could be quadratic terms or inverse terms but always go with the minimum number of parameters. Binning might be useful by your trading degrees of freedom for improving the contribution to Chi Sq from certain bins. Are there trade offs. You could also smooth the data, again what are the trade offs. If you have lots of estimates of parameters you want consistency. Finally statistical uncertainty is only part of the the uncertainty in measurements.