RL circuit differential equations

[evol_w10lv]

Homework Statement

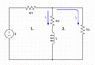
Task is to write differential equation for this circuit.
E, R1, R2, R3, L are constants.

Homework Equations

Ul = L di/dt

The Attempt at a Solution

I guess, we have to use current method for each contour.
1st contour equation:
E = U1 + U2 + Ul = i*(R1+R2) + L di/dt

Equation arround the loop:
E = i*R1 + i2*(R1+R3)

It means that I got system:
E=i*(R1+R2) + L di/dt +i2*R1
E = i*R1 + i2*(R1+R3)

The problem is i2. I need to get i2, I guess, from second contour using L, R2 and R3. Can someone help quickly? I need this task until tomorrow.
Or I have done something wrong at the begining?

 

[gneill]

Yes, you'll need to write two loop equations. I suggest choosing two of the branch currents and letting the third current be determined by KCL. Thus:

So the current through R1 is i1+i2.

If you've studied Thevenin Equivalents already you can make your life much simpler by replacing the voltage source and resistor network with its Thevenin Equivalent. Then you'll have a circuit consisting of a source, one resistor, and one inductor Otherwise, continue on the way you're going.

 

[evol_w10lv]

Using Thevenin's theorem, I will get this?

We have spoken about Thevenin's and Northon's theorems, but we haven't got any examples.
Actually, I guess, there's no matter, which way I use. I need to solve current and voltage througt inductor, that's why I have to use differential equation and U = L di/dt.

If I use Thevenin's theorem, then it should be:

L di/dt + R(Thevenin)*i = E (Thevenin)

Is it R(Thevenin) = R1 + (R2*R3)/(R2+R3) ?
What is the E (Thevenin)? :shy:

 

[gneill]

Using Thevenin's theorem, I will get this?

We have spoken about Thevenin's and Northon's theorems, but we haven't got any examples.
Actually, I guess, there's no matter, which way I use. I need to solve current and voltage througt inductor, that's why I have to use differential equation and U = L di/dt.

If I use Thevenin's theorem, then it should be:

L di/dt + R(Thevenin)*i = E (Thevenin)

Yup.

Is it R(Thevenin) = R1 + (R2*R3)/(R2+R3) ?

[STRIKE]Yup.[/STRIKE] Correction: That would be the Thevenin resistance as seen from the voltage source (assuming the resistance of the inductor is zero). You want the resistance seen looking into the circuit from the inductor's location. Sorry about that.

What is the E (Thevenin)? :shy:

If you temporarily remove the inductor and measure the open-circuit voltage there, what would you get?

 

[evol_w10lv]

Do you mean:
E (Thevenin) = (E*R2)/(R1+R2) ?

 

[gneill]

Do you mean:
E (Thevenin) = (E*R2)/(R1+R2) ?

Not quite. R1 and R3 form the voltage divider. With the inductor out of the circuit, R2 is presented with an open circuit at the "inductor end", so no current flows through it.

It might help to remember that the two branches (the one with R3 and the one with R2) are in parallel, so you are free to exchange their positions. That will make the voltage divider comprising R1 and R3 more obvious.

 

[evol_w10lv]

Then it has to be:
E (Thevenin) = (E*R3)/(R1+R3)
Or again I have made akward mistake? :D

And after that:
(E*R3)/(R1+R3) = (R1 + (R2*R3)/(R2+R3))*i + L di/dt.

 

[gneill]

Then it has to be:
E (Thevenin) = (E*R3)/(R1+R3)
Or again I have made akward mistake? :D

And after that:
(E*R3)/(R1+R3) = (R1 + (R2*R3)/(R2+R3))*i + L di/dt.

One small correction. Back in post #4 I Okay'd your Thevenin resistance but misremembered the placement of the resistor labels. It turns out that "shape" of your expression is correct but it actually gives the Thevenin resistance of the circuit as "seen" from the voltage source rather than looking into the circuit from the inductor's location. Fix that up and you're good to go.

 

[evol_w10lv]

Yes, of course.
In that case: R(Thevenin) = R2 + (R1*R3)/(R1+R3)

And equation:
(E*R3)/(R1+R3) = (R2 + (R1*R3)/(R1+R3))*i + L di/dt.

And I've got another question. If there is no R3 before comutation proces (t<0), then I(0) = E/(R1+R2)?

 

[gneill]

Yes, of course.
In that case: R(Thevenin) = R2 + (R1*R3)/(R1+R3)

And equation:
(E*R3)/(R1+R3) = (R2 + (R1*R3)/(R1+R3))*i + L di/dt.

And I've got another question. If there is no R3 before comutation proces (t<0), then I(0) = E/(R1+R2)?

How does an inductor behave when a sudden change of potential happens? If you suppose that the current for t < 0 is zero, when the voltage source is suddenly turned on what's the current through an inductor at time t = 0⁺ ?

 

[evol_w10lv]

Hmm.. I guess, then initial condition (current through inductor) I = 0, when (t=0). Am I wright?
And, when t>0, then current will be solution of equation, which we wrote:
((E*R3)/(R1+R3) = (R2 + (R1*R3)/(R1+R3))*i + L di/dt.).

 

[gneill]

Hmm.. I guess, then initial condition (current through inductor) I = 0, when (t=0). Am I wright?

Yes that's right.

And, when t>0, then current will be solution of equation, which we wrote:
((E*R3)/(R1+R3) = (R2 + (R1*R3)/(R1+R3))*i + L di/dt.).

Sure.

 

[evol_w10lv]

And also..
To get voltage through inductor (t>0), I have to integrate result of current?
And, when I have voltage, to get current, I have to derive result of voltage?

 

[gneill]

And also..
To get voltage through inductor (t>0), I have to integrate result of current?
And, when I have voltage, to get current, I have to derive result of voltage?

I'm not sure what you're getting at here, but once you've solved the differential equation for i(t) you can write the voltage across the resistor using Ohm's law, then the voltage across the inductor using KVL.

 

[evol_w10lv]

Never mind.
Actually this task is solved. Thanks for helping me. :)

 

[evol_w10lv]

Hei!
Again it's me. Can you chek these two tasks?
1.

System of:
L*di_L/dt + R1*(I_L - I_2) = V
R1*(I_2 - I_L) + (R_2+R_3)*I_2=0

from second equation: I_2 = (R1*I_L)/(R1+R2+R3)
then:
L*di_L/dt + R1*(I_L - (R1*I_L)/(R1+R2+R3)) = E

And if I use Thevenin method, then:
R(Thevenin) = ((R2+R3)*R1)/(R1+R2+R3)
E(Thevenin) = V

L*di_L/dt + (((R2+R3)*R1)/(R1+R2+R3))*I_L = V

2.

R(Thevenin) = R3 * ((R1*R2)/(R1+R2))
E(Thevenin) = (V*R2)/(R2+R1)

L*di_L/dt + (R3 * ((R1*R2)/(R1+R2)))*I_L = (V*R2)/(R2+R1)

And what do you suggest, when current source given?
Hope that you'll chek the tasks. I guess, it's boring for you so easy tasks. I tried to solve by myself, but I can't chek whether they are correct. :)

 

[gneill]

It is preferred that a new thread be started for each new question rather than tacking onto an old thread. Please keep that in mind for the future.

The first one looks fine. The second one has a problem with R(Thevenin); R3 is in series with the parallel combination of R1 and R2.

 

[evol_w10lv]

Ohh.. of course about second one.. typing mistake.
OK, next time I'll make new topic. Just thought.. almost same circuit and same task.

 

[gneill]

Ohh.. of course about second one.. typing mistake.
OK, next time I'll make new topic. Just thought.. almost same circuit and same task.

No worries. Looks like you've got the hang of these problems. Well done.