Franklie001
- 49
- 7
- Homework Statement
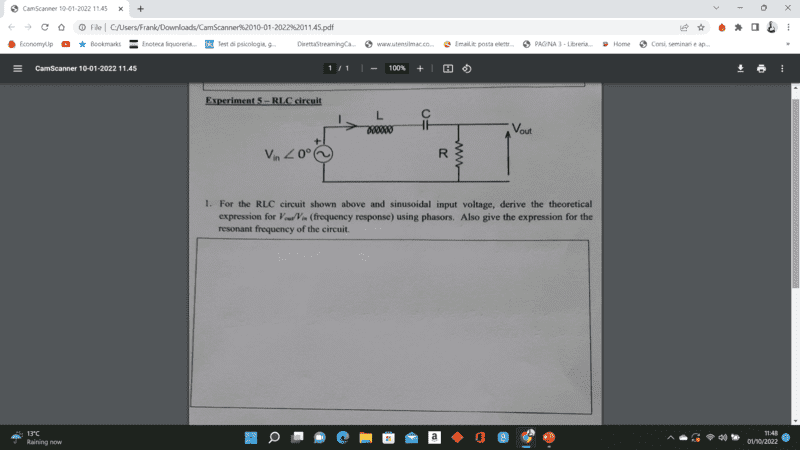
- For the RLC circuit shown above and sinusoidal input voltage, derive the theoretical expression for Vout/Vin (frequency response) using phasors. Also, give the expression for the resonant frequency of the circuit.
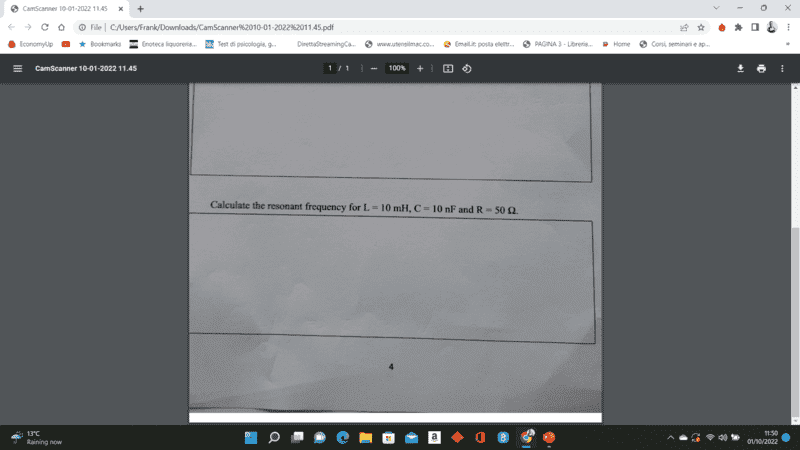
Calculate the resonant frequency for L=10mH, C=10nF, R=50 ohm
- Relevant Equations
- Vout/Vin
Good morning,
I need some help solving those two question. I've attached my attempted solution below. Could i solve the transfer function any further?
Thank you for your help
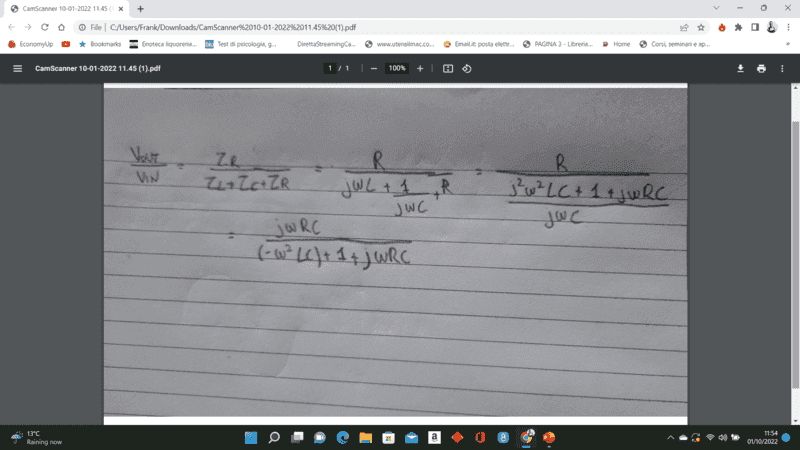
I need some help solving those two question. I've attached my attempted solution below. Could i solve the transfer function any further?
Thank you for your help