SUMMARY
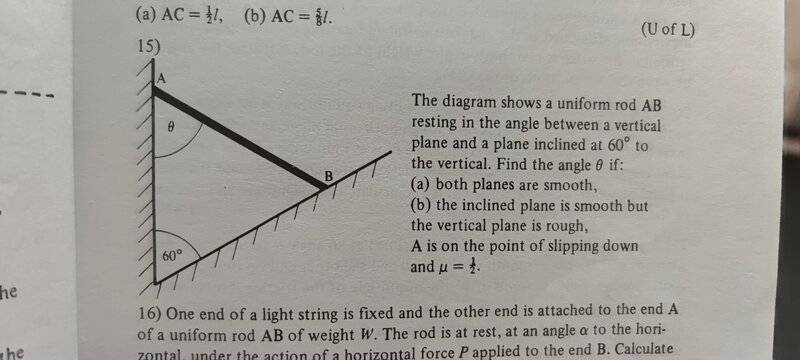
The discussion centers on the analysis of a rod in equilibrium and determining its angle to the vertical plane. Participants emphasize the importance of creating a free body diagram to visualize the forces acting on the rod. This foundational step is crucial for applying principles of static equilibrium, allowing for the calculation of angles and forces effectively. The conversation highlights that understanding the forces involved is essential for solving such problems accurately.
PREREQUISITES
- Static equilibrium principles
- Free body diagram creation
- Basic trigonometry for angle calculations
- Understanding of forces (tension, weight)
NEXT STEPS
- Study the principles of static equilibrium in detail
- Practice drawing free body diagrams for various scenarios
- Learn how to apply trigonometric functions to solve for angles
- Explore case studies involving rods and beams in equilibrium
USEFUL FOR
Students in physics or engineering, educators teaching mechanics, and anyone interested in understanding the principles of static equilibrium and force analysis.