bassguitar
- 5
- 0
Homework Statement
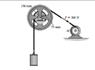
If the motor M exerts a constant force of P = 300 N on the cable wrapped around the reels outer rim, determine the velocity of the 50 kg cylinder after it has traveled a distance 2 m. Initially the system is at rest. The reel has mass 25 kg, and the radius of gyration about its center of mass A is ka = 125 mm.
Homework Equations
Ia = ma*k2a
Ia*α = ΣM
The Attempt at a Solution
Ia = ma*k2a = 25*0.1252 = 0.390625 kgm2
Ia*α = ΣM = -P*ro + mgri = -300*0.15 + 50*9.81*0.075 = -8.2125kgm
α = -8.2125 / 0.390625 = -21.024rad/s2
a = α*ri = -1.5768m/s2
s = (at2)/2 and v = at and we get that v = 2.51m/s, but the answer given is 1.91m/s.
What am I doing wrong? In the solution they use energy method which I understand, but I should be able to solve it correctly that way as well. Why do I get a different answer?