Ene Dene
- 47
- 0
Homework Statement
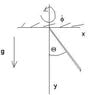
The rod of length 2a swings and it rotates \dot{\phi}[/tex]. Find kinetic energy.<br /> <h2>The Attempt at a Solution</h2><br /> <br /> I know how to find kinetic energy if we have rotation just in xy plane, but I'm having a problem to understand how to do it with rotation around y axis.<br /> <br /> If we have rotation in xy plane:<br /> x_{cm}=asin(\theta)<br /> y_{cm}=acos(\theta)<br /> \dot{x}_{cm}=acos(\theta)\dot{\theta}<br /> \dot{y}_{cm}=-asin(\theta)\dot{\theta}<br /> E_{kin}=\frac{1}{2}m(\dot{x}_{cm}^2+\dot{y}_{cm}^2)+\frac{1}{2}m\cdot\frac{1}{12}(2a)^2\dot{\theta}^2<br /> E_{kin}=\frac{2}{3}m\dot{\theta}^2<br /> <br /> For rotation around y, I assume that we have translation component in z direction, and rotation component.<br /> z_{cm}=asin(\theta)sin(\phi)<br /> Is this correct? (look at the picture)<br /> \dot{z}_{cm}=a(cos(\theta)sin(\phi)\dot{\theta}+cos(\phi)sin(\theta)\dot{\phi})<br /> E_{z}=\frac{1}{2}m\dot{z}_{cm}^2+\frac{1}{2}I_{cm}\dot{\phi}^2.<br /> Rotation part of E_{z} bothers me, maybe I have to multiply it by (lsin(\theta))^2.
Attachments
Last edited: