Rotational Dynamics, centre of mass.

[fundoo]

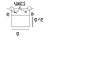
Homework Statement

A uniform plate of mass m is suspended in the way shown. determine immediately after the connection at B has been released ;:
A) angular aceleration of plate
B) acceleration of its centre of mass

Homework Equations

before b is detached
t1 + t2 = mg (Linear equillibrium)
t1 x c/2 = t2 x c/2 (rotational eqb)
so t1 = t2 = mg/2

The Attempt at a Solution

immediately after B is opened ::
axis of rotation thru A. for Torque of mg = mg x c/2 ....1
also torque = Ia = moment of intertia x angular acceleration = (1/2 x m(c² + c²/4) + 5mc²/4) x a

so 'a' = 1.2g/c

but that is not the answer.If you could please explain the Theory Involved and a general approach to solve the questions, i would be very thankful.

 

[cryptoguy]

the pivot point is going to be the upper left corner of the disk, right? You got to remember that the torque is not going to = mg or mg x c/2. You need to consider only the part of the gravitational force perpendicular to the lever arm (whose length you will need to figure out, it is the length from the center to the A corner of the plate).

 

[fundoo]

dont we consider the perpendicular length from the centre of mass, so that will be c/2.

now even if we take the distance from centre to left corner, it will be c²/4 + c²/16 = 5c²/16.

so torque will be mg x $$\sqrt{5}$$c/4

and equating it to Ia = (5mc²/8 + 5mc₂/4)a

gives a = 2$$\sqrt{5}$$g/15c

but the actual answer given is 24g/17c.

PLEASE HELP.