B Rotational Dynamics: Confused about the tension in this string pulling a mass up an incline

[Sep]

TL;DR Summary

I am confused why the solutions say that Mgsin(theta) is greater than tension. Isn't tension greater because the block is going up the incline? Or is it that in cases where the block is decelerating but still going up, the force of gravity will be greater?

Question

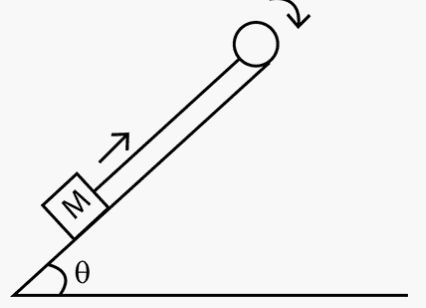
A wheel of radius r and moment of inertia I about its axis is fixed at the top of an inclined plane of inclination θ as shown in the figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. Initially, the wheel is rotating at a speed of ω in a direction such that the block slides up the plane. How far will the block move before stopping?​

Suppose the deceleration of the block is a. The linear deceleration​

of the rim of the wheel is also a. The angular deceleration of the​

wheel is α=ar. I the tension in the string is T, the equations of​

motion are as follows:​

Mgsinθ−T=Ma (This is the part that I am confused about)​

and Tr=Iα=Iar​

Eliminating T from these equations​

Mgsinθ−Iar2=Ma​

giving a=Mgr2sinθI+Mr2​

I am confused why the solutions say that Mgsin(theta) is greater than tension. Isn't tension greater because the block is going up the incline? Or is it that in cases where the block is decelerating but still going up, the force of gravity will be greater?

 

[Nugatory]

Isn't tension greater because the block is going up the incline?

The block has positive velocity upwards, but that has nothing to do with the tension. Consider that if we cut the string the block would still keep coasting up the ramp for a while, until gravity brought it to a stop and started it back down.

 

[Sep]

The block has positive velocity upwards, but that has nothing to do with the tension. Consider that if we cut the string the block would still keep coasting up the ramp for a while, until gravity brought it to a stop and started it back down.

Oh, I understand now. The initial velocity. Thank you so much!