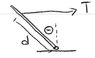
The discussion centers on understanding torque in rotational equilibrium, particularly the signs of torque contributions from gravity and tension. It is clarified that one torque must be considered positive while the other is negative due to their opposing rotational effects—gravity induces clockwise rotation while tension induces counterclockwise rotation. The confusion regarding the role of friction and normal forces is addressed, explaining that their moments are zero when taking moments around the origin. The participants also discuss the application of the cross product and the anticommutative property, which explains the sign differences in torque calculations. Overall, the conversation emphasizes the importance of directionality and reference points in analyzing rotational systems.