merbear
- 9
- 0
[SOLVED] Rotational Kinetic Energy and distribution of diatomic molecules
a) Calculate the total rotational kinetic energy of the molecules in 1.00 mol of a diatomic gas at 300 K.
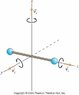
b) Calculate the moment of inertia of an oxygen molecule (O2) for rotation about either the x- or y-axis shown in the figure. Treat the molecule as two massive points (representing the oxygen atoms) separated by a distance 1.21×10-10m. The molar mass of oxygen atoms is 16 g/mol.
c) Find the rms angular velocity of rotation of an oxygen molecule about either an x- or y-axis
kT=2/3*<k>
where, k is boltzman constant and K is kinetic energy
I=mR^2
E(rot)= 1/2*I*angular velocity(for x)^2 + 1/2*I*angular velocity(for y)^2
To find the answer to the first part of the problem I used the first equation listed and got 6.21E-21 J, but that answer is incorrect. I do not know how else to approach the problem. I think it went wrong because K in that equation is the average kinetic energy and not the rotational kinetic energy, but I couldn't find another equation that would work.
For the second part I used I=mR^2. To find m, I took the molar mass and divided by avagadros number and I used the distance given for R.
my answer was: 3.89E-46 kg*m^2, but I don't think that was correct.
For the third part, I would think that you would use Vrms equals the squareroot of (3kT/m). But we are not given the temperature. So I don't know how to go about this part either.
I would really appreciate help on these three parts. Thank you!
a) Calculate the total rotational kinetic energy of the molecules in 1.00 mol of a diatomic gas at 300 K.
b) Calculate the moment of inertia of an oxygen molecule (O2) for rotation about either the x- or y-axis shown in the figure. Treat the molecule as two massive points (representing the oxygen atoms) separated by a distance 1.21×10-10m. The molar mass of oxygen atoms is 16 g/mol.
c) Find the rms angular velocity of rotation of an oxygen molecule about either an x- or y-axis
Homework Equations
kT=2/3*<k>
where, k is boltzman constant and K is kinetic energy
I=mR^2
E(rot)= 1/2*I*angular velocity(for x)^2 + 1/2*I*angular velocity(for y)^2
The Attempt at a Solution
To find the answer to the first part of the problem I used the first equation listed and got 6.21E-21 J, but that answer is incorrect. I do not know how else to approach the problem. I think it went wrong because K in that equation is the average kinetic energy and not the rotational kinetic energy, but I couldn't find another equation that would work.
For the second part I used I=mR^2. To find m, I took the molar mass and divided by avagadros number and I used the distance given for R.
my answer was: 3.89E-46 kg*m^2, but I don't think that was correct.
For the third part, I would think that you would use Vrms equals the squareroot of (3kT/m). But we are not given the temperature. So I don't know how to go about this part either.
I would really appreciate help on these three parts. Thank you!