haydn
- 26
- 0
Homework Statement
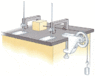
The sliding block has a mass of 0.800 kg, the counterweight has a mass of 0.460 kg, and the pulley is a hollow cylinder with a mass of 0.350 kg, an inner radius of 0.020 m, and an outer radius of 0.030 m. The coefficient of kinetic friction between the block and the horizontal surface is 0.250. The pulley turns without friction on its axle. The light cord does not stretch and does not slip on the pulley. The block has a velocity of 0.820 m/s toward the pulley when it passes through a photogate.
(a) Use energy methods to predict its speed after it has moved to a second photogate, 0.700 m away.
Homework Equations
KET = (1/2)mv2
KER = (1/2)Iw2
I for a hollow cylinder = (1/2)M(R12 + R22)
w = omega = angular velocity
The Attempt at a Solution
I know work is equal to the change in kinetic energy so I go:
W = ((1/2)(M1+M2)Vf2 + (1/2)IwF2) - ((1/2)(M1 + M2)VI2 + (1/2)Iw2 + M2gs)
and W = -f * s = - (coefficient of friction)M1gs
s = .7 as given in the problem...
So I substitute that expression for work into the first equation, solve for VF but the website I'm using is telling me I'm getting the wrong answer... what am I doing wrong?