AgentRedfield
- 10
- 0
I think I'm not understanding some conceptual part of rotational kinematics because all the questions seem connected. I want to figure it out as best I can so please don't solve it but any hints in the right direction would be really appreciated, thanks!
The Question:
A stiff piece of wire is bent into a circle and mounted (vertically) to rotate as shown. A wooden bead with a hole through its center can slide frictionlessly on that wire. The radius of the wire hoop is 15.0 cm and it rotates steadily with a period of 0.450 s
.
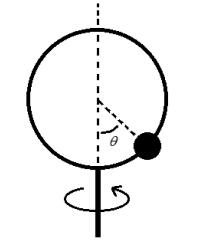
a) At what angle θ will the bead rotate, along with the hoop, without sliding (up or down)? Show that there are two possible angles (solutions) for this hoop size and rotational speed. Include a clear free body diagram of the bead as part of your solution.
b) At what period would the ball not leave the bottom position (θ =0)?
c) At what period would θ =90 degrees? What would that angular speed then be? Explain, in terms of forces on the bead, why one can’t spin the hoop fast enough for the bead to reach θ =90 degrees.
d) If the hoop were twice the radius, what would be the non-zero angle (at which the bead would rotate)?
Relevant Equations:
Fg=mg
a=mv2/r
v=wr
w=(2*pi)/T
Attempt at solving:
a) If the bead is at θ then there is a normal force directed towards the center of the circle and the force of gravity directed downward. Sum of forces in the 'y' gives Ncosθ-Fg=0 and in 'x' is Nsinθ=ma
I think the acceleration is rw2 so lots of substitution gives θ=tan-1 (rw2 /g)
θ=71.47 degrees
This answer seems reasonable but I'm not sure if I skipped something. Also I don't know how to find the second angle.
b) I think Fg=N but if θ is zero it seems like acceleration would be zero so period would be zero which makes no sense.
c) Normal force would be zero and Fg=mv2/r
so g=rw2 and w=2pi/T, after substitution I got:
w=8.08 rad/s2
T=0.777 s
I think I'm missing the conceptual part of c because my answer seems like normal numbers.
d) I imagine this would be solved the same as part a but the question seems to imply it would only have one angle it rotates at, what changed?
Thanks again for your time and help!
The Question:
A stiff piece of wire is bent into a circle and mounted (vertically) to rotate as shown. A wooden bead with a hole through its center can slide frictionlessly on that wire. The radius of the wire hoop is 15.0 cm and it rotates steadily with a period of 0.450 s
.
a) At what angle θ will the bead rotate, along with the hoop, without sliding (up or down)? Show that there are two possible angles (solutions) for this hoop size and rotational speed. Include a clear free body diagram of the bead as part of your solution.
b) At what period would the ball not leave the bottom position (θ =0)?
c) At what period would θ =90 degrees? What would that angular speed then be? Explain, in terms of forces on the bead, why one can’t spin the hoop fast enough for the bead to reach θ =90 degrees.
d) If the hoop were twice the radius, what would be the non-zero angle (at which the bead would rotate)?
Relevant Equations:
Fg=mg
a=mv2/r
v=wr
w=(2*pi)/T
Attempt at solving:
a) If the bead is at θ then there is a normal force directed towards the center of the circle and the force of gravity directed downward. Sum of forces in the 'y' gives Ncosθ-Fg=0 and in 'x' is Nsinθ=ma
I think the acceleration is rw2 so lots of substitution gives θ=tan-1 (rw2 /g)
θ=71.47 degrees
This answer seems reasonable but I'm not sure if I skipped something. Also I don't know how to find the second angle.
b) I think Fg=N but if θ is zero it seems like acceleration would be zero so period would be zero which makes no sense.
c) Normal force would be zero and Fg=mv2/r
so g=rw2 and w=2pi/T, after substitution I got:
w=8.08 rad/s2
T=0.777 s
I think I'm missing the conceptual part of c because my answer seems like normal numbers.
d) I imagine this would be solved the same as part a but the question seems to imply it would only have one angle it rotates at, what changed?
Thanks again for your time and help!